Sizing a gantry gusset

Technical Communication Technical Documentation
1

Hello

I'm looking to size a gusset for a lifting gantry

Here is attached the information I calculated


gousset.png
1 Like
2

Hello

Is the 10,670 N charge precisely there?

3

Hello

the gantry crane  is equipped with a mobile pallan that carries the load of 1000Kg  so the load can be located at the extrimity

 

4

And what is the distance to the end? This data makes it possible to know the maximum stress.

1 Like
5

Is the connection between the IPE and the pole considered pivotal? (of course, this remains a hypothesis)

6

Hello

My first question is; Are you sure that the force applies at this point or is it a force distributed on the beam?

If it's a bridge load, personally (I'm probably wrong) I'd look at the intensity of the force at the end of the gusset. To do this, I would make an assessment of the actions, and I reduce everything to the same point. After that you won't have the length but it doesn't matter, leave the unknown to you. 

Normally you should have flex.

You can then use the following formula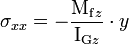\sigma_{xx} = -\frac{\mathrm{M}_{\mathrm{f}z}}{\mathrm{I}_{\mathrm{G}z}} \cdot y

For the moment of inertia you can use this formula: (b × h^3)/36

(Be careful to define the base and the height what and what.) ( from the following site : http://liengeniecivil.wifeo.com/documents/Chap-8-Caractrisques-gomtriques-des-sections-V2001.pdf )

Thanks to the moment of inertia you will be able to draw all the information about your triangle and you will be able to size it to resist the stress.

 

Obviously you don't know your sigma constraint. To solve this problem, you need to apply the Von Mises resistance criterion.

So you get the following  inequality: 

\sigma_{xx} \le \frac{\mathrm{R_e}}{s}

With Sigma xx = 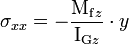\sigma_{xx} = -\frac{\mathrm{M}_{\mathrm{f}z}}{\mathrm{I}_{\mathrm{G}z}} \cdot y

Re coming from the material and s safety coef. We can put everything on one side and have the dimensions of the triangles.
 

Well that's what I'd do, but I'm cheating a bit since I'm taking a formula for a beam. 

I hope this can help you a little.

Kind regards

Ju"

 

 

2 Likes
7

Hello

It is important to know that all lifting elements in a company must be tested and checked regularly.

The test load is 1.25 x declared load for fixed hoists and 1.5 for moving hoists.

 

So a 1t moving hoist will be tested at 1.5t.

 

S.B

8

Re

The length of the beam is 3m the distance of the extrimity depends on the length of the gusser +10cm of the gusset

As far as the force is concerned, it is a mobile pallan that carries the load of 1000kg so it can be applied  to the extremity, maybe we can consider it as punctual but I don't know?

 

9

Re

The length of the beam is 3m the distance of the extrimity depends on the length of the gusser +10cm of the gusset

As far as the force is concerned, it is a mobile pallan that carries the load of 1000kg so it can be applied  to the extremity, maybe we can consider it as punctual but I don't know?

 

10

re

julien_2

how do you calculate Mfz for the gusset?

 

11

Hello again,

In the case of a pallan, yes, we can say that it is a point load.

When you do your torsor of mechanical actions, when you reduce the point load at your point you will have a moment that will appear (Force*length), following an axis it all depends on how your reference point is oriented. (For example, you with a force in y, and a length in x, you will get a moment in z).

This method takes you through the fundamental principle of statics.

http://fr.wikipedia.org/wiki/Torseur

This link can help you, look at the resulting paragraph and reduction.

So in your Mfz torsor, will be the moment following the z-axis.

2 Likes
12

Re

Julien: I'm following your path to size the gusset

I did this (attachment)

In relation to which axis do I choose my dinertie moment?

After I would give lengths all according to B or D and I will have sized my gusset

Thank you


axe.png
13

Good evening

Sorry for the delay.

I just realized what a big mistake I said. Shame on me. 

IGz is not the moment of inertia but the quadratic moment, it is calculated according to the shape of the straight section. 

This means that:

\mathrm{I}_{\mathrm{G}z} = \int_{\mathrm{S}} y^2 \cdot \mathrm{dS}

(A good link explaining http://www.geniecvl.com/rdm-la-flexion-composee/

http://fr.wikipedia.org/wiki/Flexion_(mat%C3%A9riau)

http://fr.wikipedia.org/wiki/Moment_quadratique )

 

14

Hello

For this calculation, I think we need to consider the load at the center of the beam. This also gives the maximum torque at each end.

Then, you have to size your gusset so that the tube + gusset assembly in one direction and IPE + gusset in the other direction has a sufficient intertie so that the stress in the connection is less than allowable.

Determining the necessary intertie is easily done analytically. To see what this corresponds to physically, either you draw it on CAD software and measure, or you can use Huygens' theorem to break down the calculation.

 

A little advice, on IPEs, we usually put a stiffener between the 2 wings to the right of the gusset.

 

@julien_2, the inertia is normally calculated by making b*h^3/12. Why /36?

1 Like
15

to Chamade: Because it's the formula for a triangle.

http://ecoconstruction.rpn.univ-lorraine.fr/co/Module_UVEDTEST_167.html

But I know that there is also a difference between the quadratic moment and the moment of inertia. (I need to dive back into it a little bit)

16

OK. Except that in this case the triangle is seen in profile. To calculate inertia, the cross-section is not triangular.

2 Likes
17

Yes chamade, I surrendered later.

In addition I say in my messages that we must take into account "the shape of the right section".

 And if we cut the gusset, we get a rectangle as a section. 

Sorry for the mistake anyway. (I'm going to be told about my youth haha)