Hallo aan jou,
Sta me toe een paar aanvullende informatie te geven.
De verschillende modelleringsoplossingen die voor u beschikbaar zijn, zijn:
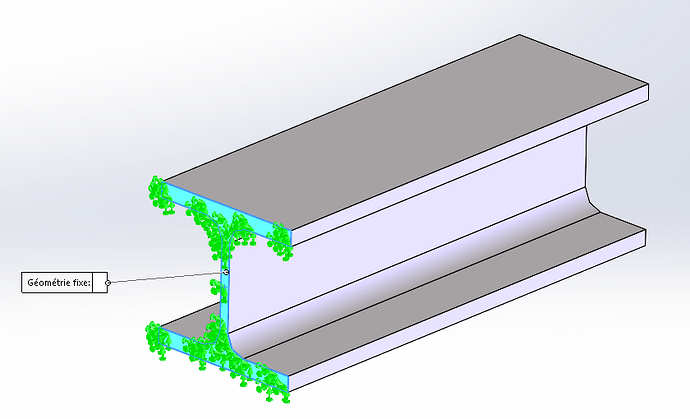
1- Straalmaas, deze theorie is alleen van toepassing als de lengte van het element groter is dan 3x de grootste afmeting van de doorsnede. A priori is dat hier het geval, en het is ook de methode die ik zal gebruiken vanwege de eenvoud/snelheid.
2- Schaalgaas, hier niet geschikt omdat uw profiel geen constante doorsnede heeft. Met een vierkante buis of rechthoekige buis zou je eventueel een balk kunnen vervangen door schelpen, waardoor je sommige recalcitrante verbindingen met andere lichamen beter zou kunnen beheren. Maar dit zijn extra klikken die hier niet handig zijn.
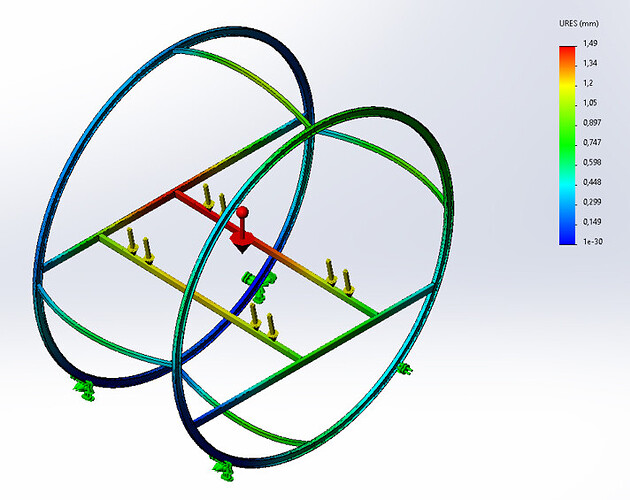
3- Volumegaas, Je hebt een vrij fijne maasverfijning nodig, die bijgevolg machinebronnen en extra rekentijd genereert, naar mijn mening nutteloos, tenzij je ermee kunt " geruststellen ".
4- Doe een buigberekening op een hoek van een tafel, in uw geval duurt het minder dan een minuut met een formulier en vinden we 89 Mpa en stof.
5- Gebruik de tool " flexformulier " die in de toolbox is geïntegreerd en die u met een paar klikken aankondigt: 89,91 Mpa
Namelijk dat al deze methoden gebruik maken van hypothesen, dus je moet " op de goede weg " zijn
En met eindige elementen proberen we alleen de foutmarge te beperken die wordt gegenereerd door aannames en discretisatie.
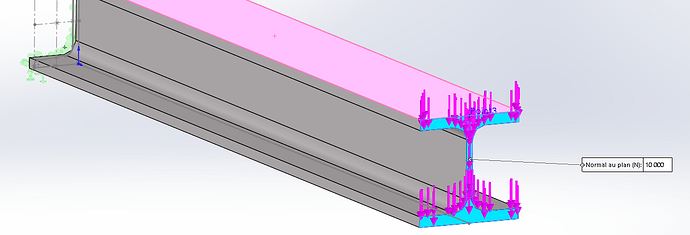
Wees voorzichtig, in je zin zeg je dat je de kracht " op het bovenvlak " van je HEB uitoefent (een verdeelde kracht?), maar in je screenshot oefen je een geconcentreerde kracht uit aan het einde van de straal. Ik laat je controleren welke de juiste is!
NB1: vergeet ook het zwaartekrachtveld niet, dat zorgt voor het gewicht van je element!
NB2: laden op afstand is erg praktisch als je niet alles hoeft te modelleren en je wilt voorkomen dat je een krachtbalans moet maken om de uitgeoefende krachten terug te brengen naar de plek waarin je geïnteresseerd bent. Hier is het duidelijk nutteloos.
Ik hoop dat ik je heb geholpen.