Hydrostatic pressure on an inclined plane

Simulation
1

Hello

I want to check with SW the water pressure force on an inclined plane. When I do the simulation on a vertical surface, SW gives me a resultant force equal to my theoretical formula: F = 1/2 x ρ x g x H² x L with H the height of my plane (and also my water height) and L its width.

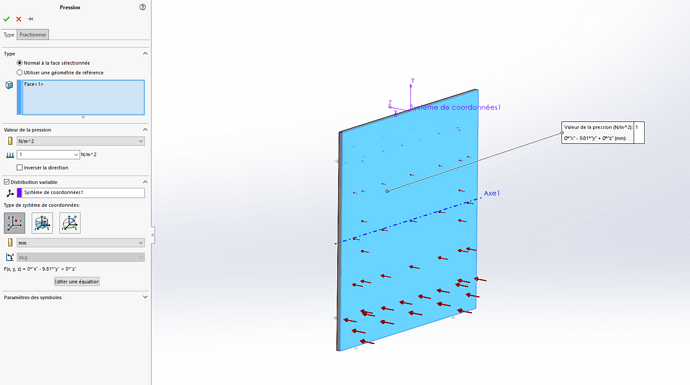
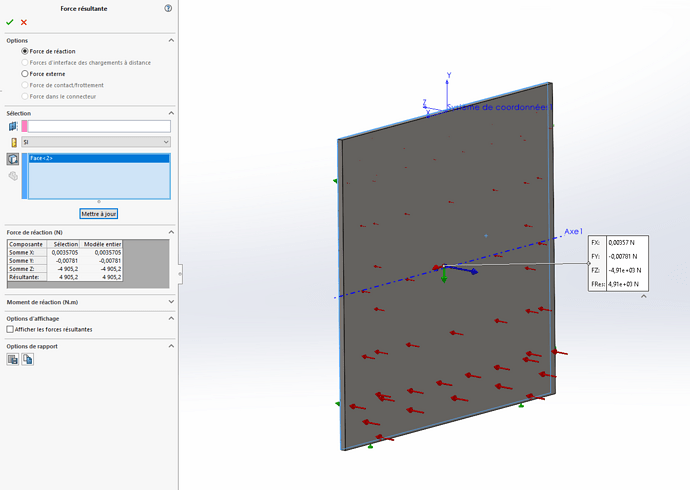
I simulated it with a 1 m x 1 m plane with a hydrostatic pressure that starts from the top of my plane:

image
image1567×875 150 KB

The simulation gives me a resultant force of 4905 N which corresponds to the calculation: 1/2 x 1000 x 9.81 x 1² x 1 = 4905 N

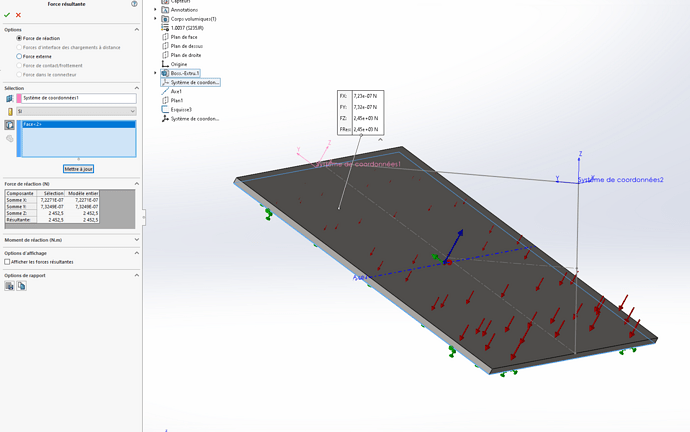
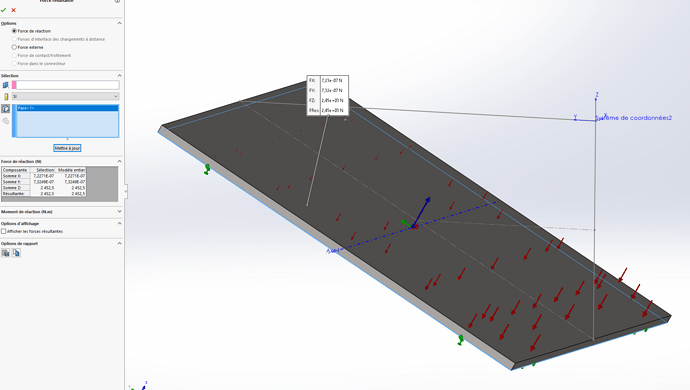
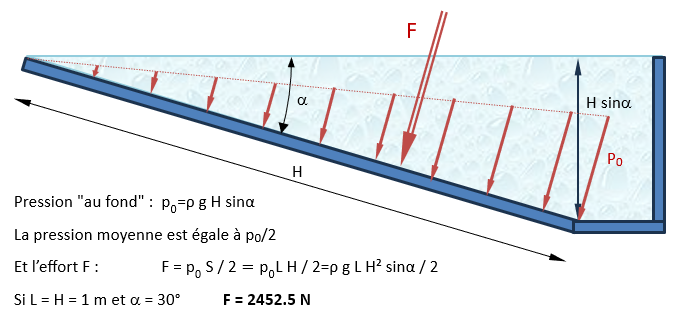
image
image1345×957 123 KB

However, when I consider my 60° inclined plane, I create my new coordinate system (No. 2) to be able to configure my pressure. The pressure is proportional to my altitude, which this time is along the Z axis of my new coordinate system:

image
image1674×1050 217 KB

In this case, my theoretical calculation tells me: F = 1/2 x ρ x g x H x h x L cos(α) with H the height according to my Z axis (0.5 m in my case) and h the height of the inclined plane (1 m). So: F = 1/2 x 1000 x 9.81 x 0.5 x 1 x 1 x cos (60°) = 1226 N
But when I calculate SW I find: 2452 N

image
image1869×1058 233 KB

SW gives me double. We know that cos(60°) = 0.5 so it comes from there, but I don't understand why SW doesn't get the right result with these parameters. I thought it could come from my pressure, but it is well applied according to my Z altitude of my coordinate system 2...

I'm stalling the... Any ideas?

2

Hello

Stupid hypothesis, as you are inclined, your pressure creates two components: a horizontal one but also a vertical one (zero when the wall is vertical). SW must give you the resulting force which is the sum of your two forces (we can see the 2 arrows by the way: the blue one which is the normal force on the wall and the green one which is the component directed in the direction of the slope). I didn't do any calculations but your concern may come from there.

3

Good evening

There simply seems to be one coefficient too many in your expression of effort, as you choose: 0.5, or 1/2 or cos(60°)...
Hence the result half that of the simulation.
image

1 Like
4

Hello

Yes I found my mistake, it's a misinterpretation of my formula. When I wrote:

F = 1/2 x ρ x g x H x h x L cos(α) with H the height according to my Z axis (0.5 m in my case) and h the height of the inclined plane (1 m)

I had calculated the height H by applying my cos60 (i.e. 0.5) when I shouldn't have it. That's why I had a result that was 2 times lower. The right formula is:

F = 1/2 x ρ x g x H x W cos(α), where H is the height of the inclined plane (1 m), L is the width (1 m)

Thank you for the insight that allowed me to identify my mistake.

1 Like