Hydrostatische druk op een hellend vlak

[guillaume.luquet]

Hallo

Ik wil met SW de waterdrukkracht op een hellend vlak controleren. Als ik de simulatie op een verticaal oppervlak doe, geeft SW me een resulterende kracht die gelijk is aan mijn theoretische formule: F = 1/2 x ρ x g x H² x L met H de hoogte van mijn vliegtuig (en ook mijn waterhoogte) en L de breedte.

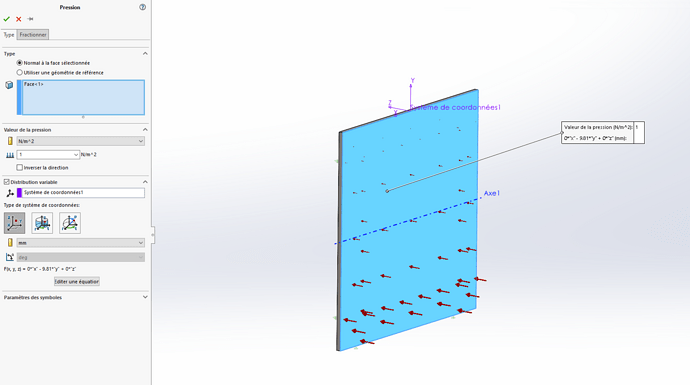
Ik heb het gesimuleerd met een vliegtuig van 1 m x 1 m met een hydrostatische druk die begint vanaf de bovenkant van mijn vliegtuig:

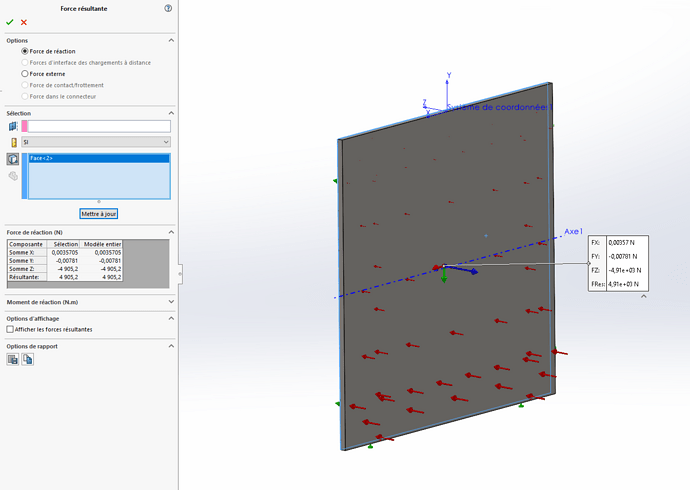
De simulatie geeft me een resulterende kracht van 4905 N die overeenkomt met de berekening: 1/2 x 1000 x 9,81 x 1² x 1 = 4905 N

Als ik echter rekening houd met mijn hellend vlak van 60°, creëer ik mijn nieuwe coördinatensysteem (nr. 2) om mijn druk te kunnen configureren. De druk is evenredig met mijn hoogte, die deze keer langs de Z-as van mijn nieuwe coördinatensysteem is:

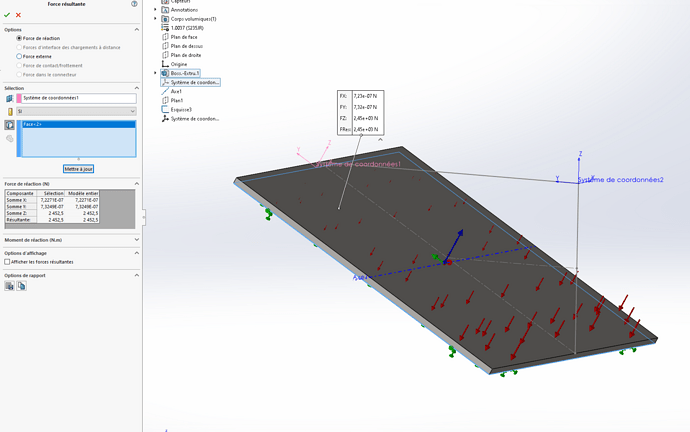
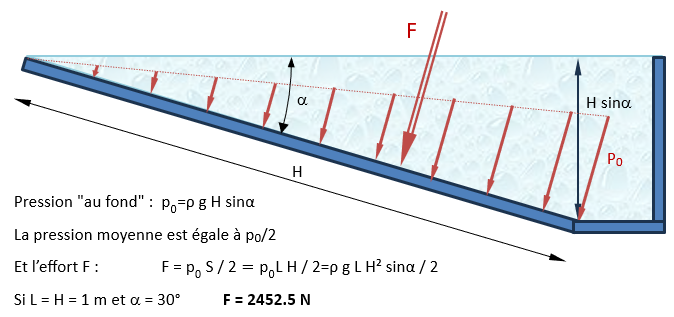
In dit geval zegt mijn theoretische berekening me: F = 1/2 x ρ x g x H x h x L cos(α) met H de hoogte volgens mijn Z-as (0,5 m in mijn geval) en h de hoogte van het hellend vlak (1 m). Dus: F = 1/2 x 1000 x 9,81 x 0,5 x 1 x 1 x cos (60°) = 1226 N
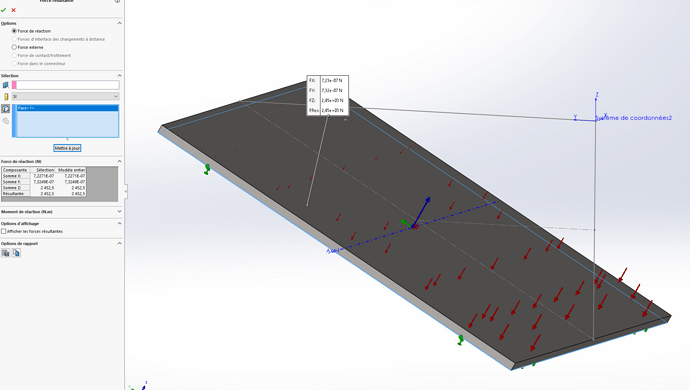
Maar als ik SW bereken vind ik: 2452 N

SW geeft me het dubbele. We weten dat cos(60°) = 0,5, dus het komt daar vandaan, maar ik begrijp niet waarom SW niet het juiste resultaat krijgt met deze parameters. Ik dacht dat het van mijn druk kon komen, maar het wordt goed toegepast volgens mijn Z-hoogte van mijn coördinatensysteem 2...

Ik stel de... Om het even welke ideeën?

[froussel]

Hallo

Stomme hypothese, zoals je geneigd bent, creëert je druk twee componenten: een horizontale, maar ook een verticale (nul als de muur verticaal is). SW moet je de resulterende kracht geven die de som is van je twee krachten (we kunnen trouwens de 2 pijlen zien: de blauwe die de normaalkracht op de muur is en de groene die de component is die in de richting van de helling is gericht). Ik heb geen berekeningen gemaakt, maar uw bezorgdheid kan daar vandaan komen.

[m_blt]

Goedenavond

Er lijkt gewoon één coëfficiënt te veel te zijn in uw uitdrukking van inspanning, zoals u kiest: 0,5, of 1/2 of cos (60°)...
Vandaar dat het resultaat de helft is van dat van de simulatie.

[guillaume.luquet]

Hallo

Ja, ik heb mijn fout gevonden, het is een verkeerde interpretatie van mijn formule. Toen ik schreef:

F = 1/2 x ρ x g x H x h x L cos(α) met H de hoogte volgens mijn Z-as (0,5 m in mijn geval) en h de hoogte van het hellend vlak (1 m)

Ik had de hoogte H berekend door mijn cos60 (d.w.z. 0,5) toe te passen terwijl ik die niet zou moeten hebben. Daarom had ik een resultaat dat 2 keer lager was. De juiste formule is:

F = 1/2 x ρ x g x H x B cos(α), waarbij H de hoogte van het hellend vlak is (1 m), L de breedte (1 m)

Bedankt voor het inzicht dat me in staat stelde mijn fout te identificeren.