Problème dimensionnement d'impact entre pièces

Out of category
,
1

Bonjour,

J’ai un petit soucis de dimensionnement de structure et j’aimerais vos avis éclairés avant de faire un retour.
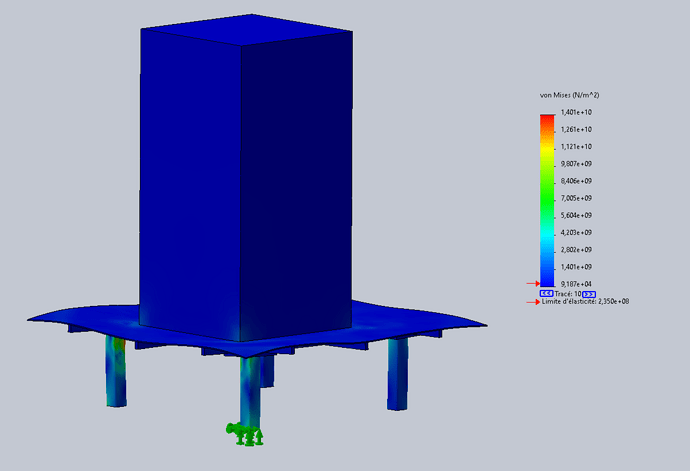
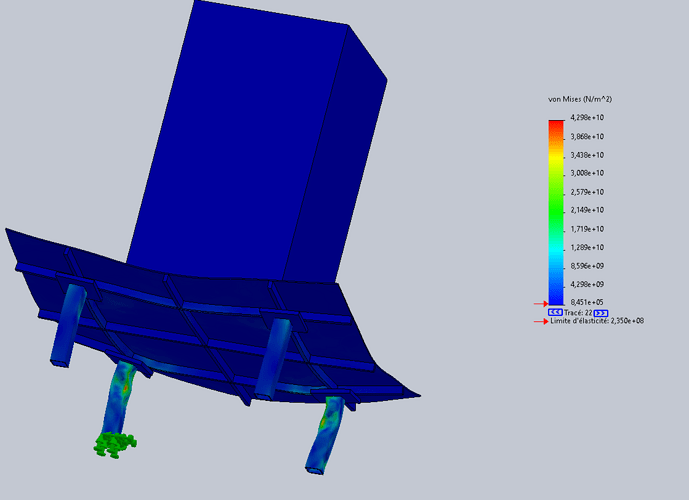
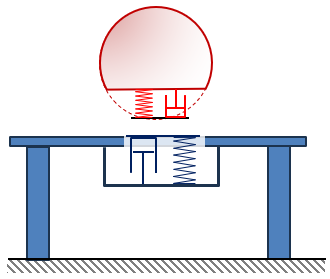
Je dois réaliser une « table » (basiquement une plaque renforcée avec 4 pieds) devant supporter la chute d’une masse de 1.1T depuis une hauteur de 10 mètres.
Mon soucis étant que j’arrive à obtenir une valeur de l’Energie Cinétique au moment de l’impact, en joules donc, mais Solidworks me demande une valeur en Newton.
J’ai bien compris qu’il fallait un essai en réel pour relever la déformée et en ressortir la valeur en N, mais cela m’est impossible à réaliser.
Existe-t-il un « tour de passe-passe » permettant d’encadrer déjà une valeur approximative de la force à appliquer?
Merci bien
TABLE V2.SLDPRT (283,1 Ko)

2

Bonjour,

J’ai regardé sur les sites qui propose de la conversion d’unités et :
1 joules = 1 Nm.

Parfois on cherche compliqué…

Cordialement.

1 « J'aime »
3

Bonjour,
Oui c’est ce que j’avais vu, mais si j’isole les N il me reste à trouver la distance m qui doit être pour moi la déformée (J/m=N). Ce que je n 'ai pas… ou bien en effet je vais chercher trop loin…

4

Bonjour,

C’est un problème d’amortissement.
La distance m dépend justement de la souplesse de ta table, donc de la déformation que tu va choisir d’admettre.

5

Bonjour,

C’est un calcul de dynamique rapide. Il y a des logiciels spécialisés pour cela (genre ceux utilisés pour les crashtests de voitures).
Le comportement des matériaux au choc peut être assez différent que lors d’un essai de traction quasi statique.

6

Je pourrais par exemple partir sur une déformation max acceptable de 1/300 comme en structure? Je vais faire un test merci

7

oui un logiciel est proposé dans 3DXperience il me semble, mais mon bureau n’a evidement pas les budgets …

8

Bonjour,
Au terme d’une chute de 10m, l’énergie cinétique de la masse est de l’ordre de 108e+3 J, énergie qui devra être dissipée entre le moment de la prise de contact et l’immobilisation de l’ensemble.
La question qui se pose est la suivante : quels sont les éléments qui contribuent à cette dissipation?

On peut imaginer que la « table » est une structure en acier, au comportement élastique relativement raide.

Mais rien n’est précisé sur la masse de chute.
S’il s’agit d’une boule de pâte à pizza (grosse, je vous l’accorde), elle aura la capacité d’absorber l’essentiel de l’énergie cinétique par sa très importante déformation élasto-visco-plastique. C’est un choc « mou ».
S’il s’agit d’une Twingo (ou d’une Fiat 500) lâchée du 3ème étage d’un immeuble, la déformation de la voiture sera sans doute moins importante que celle du pâton de pizza, et la table s’en trouvera plus fortement sollicitée.
S’il s’agit d’une boule d’acier, on se rapproche d’un choc « dur ». La table et la boule devront se répartir la dissipation, avec des efforts beaucoup plus élevés que dans les cas précédents, du fait de leurs raideurs respectives importantes.

Un modèle dynamique simple peut-être élaboré, sur la base d’une interface de contact constituée de ressorts et amortisseurs. Toute la difficulté consiste à donner des valeurs à leurs raideurs et facteurs d’amortissement.
image

Il faudrait en savoir davantage sur la nature et la structure de la table et de la masse mobile, pour tenter d’estimer ces coefficients…
Cordialement.

7 « J'aime »
9

Bonjour,

Il semble qu’il soit possible de réaliser une simulation de votre problème directement sur solidworks.
seulement dispo à partir d’une licence simulation professionnel au minimum.

1 « J'aime »
10

Bonjour, on a la simulation Premium et pro, mais la seule chose qu’ils proposent c’est une simulation de chute de l’objet en lui même sur un sol qui lui n’est pas analysé. Ce qui m’intéresse moi c’est la chute d’un objet sur mon objet d’analyse.

11

si je ne me trompe pas, une fois que l’analyse de la chute est faite, tu peux faire clic droit sur « contrainte » sous résultat et sélectionner l’outils « sonder ».

comme ça tu pourras voir la contrainte max.

avec cette contrainte max tu peux refaire une simulation en statique.

je n’ai que le module de simulation standard je n’ai pas du tout pu vérifier ce que je te dis !
(mais c’est comme ça que j’aurais fait)

12

là il s’agit de voir comment ma structure réagit lors de l’impact d’une caillasse d’une tonne, pas de voir comment ma structure réagit lorsqu’elle tombe.
Comme d’habitude, on me demande de vérifier une structure qui a déjà été construite à la va-vite … me doute que ca ne passe pas du tout mais je souhaite tout de même pouvoir fournir un résultat fiable, et même savoir comment faire pour ma culture pro…
J’ai mis la pièce TQC en PJ dans mon premier post

13

Bonjour,
j’ai mis la pièce en PJ dans mon 1er post.
Concernant la masse qui vient impacter, il s’agit de minerai de fer. On peut considérer qu’il est suffisamment aggloméré pour ne pas se déformer à l’impact…

14

J’ai trouvé ça si ça peux t’aider:

15

Yeah! je regarde ca de suite :wink: merci

16

En soit c’est juste le mouvement relatif qui est inversé.
Je ne sais pas comment on paramètre ce genre d’étude sur SW, mais de faire chuter la table avec une vitesse suffisante pour qu’elle ai une énergie cinétique équivalente ?

17

Yeap j’y ai pensé , j’essaye ca dès que possible :wink: Merci

18

oui mais l’effort sera sur les pieds et non sur le plan de travail?

19

Bonjour,
Vous avez d’autres informations sur la forme… de votre objet qui viendra en collision avec votre table déjà calculée ?
J’ai réalisé une forme simplifiée pour avoir la masse de une tonne, j’ai une section de 0.26 m², la hauteur compatible je l’obtiens avec la densité. A la base S235 pour votre table et pour le projectile.

les valeurs que vous avez fournies : une masse de 1,1 tonne (1100 kg) et une hauteur de chute de 10 mètres.

Tout d’abord, calculons la vitesse au moment de l’impact en utilisant la formule de la conservation de l’énergie mécanique :

m * g * h = (1/2) * m * v^2

où m est la masse (1100 kg), g est l’accélération due à la gravité (9,8 m/s^2) et h est la hauteur de chute (10 mètres).

1100 kg * 9,8 m/s^2 * 10 m = (1/2) * 1100 kg * v^2

107800 J = 550 v^2

En résolvant cette équation, nous pouvons trouver la valeur de la vitesse v :

v^2 = 107800 J / 550 kg v^2 ≈ 196.18 m^2/s^2 v ≈ √196.18 m/s v ≈ 14 m/s

Je suis d’accord avec les joules de la réponse précédente.
Et en première approche ce sont les pieds le problème premier …

image
image1203×822 82.6 KB

Spectrum.

P.S/

Temps de chute = √(2 * hauteur / g)

où hauteur est la hauteur de chute (10 mètres) et g est l’accélération due à la gravité (environ 9,8 m/s^2).

En substituant les valeurs dans la formule, nous obtenons :

Temps de chute = √(2 * 10 m / 9,8 m/s^2) Temps de chute ≈ √(2.04 s^2) Temps de chute ≈ 1.43 s

Donc, la durée de la chute de l’objet est d’environ 1.43 secondes.

image
image1119×812 103 KB

2 « J'aime »
20

c’est pas faux…