Probleem met de impact sizing tussen onderdelen

Out of category
,
1

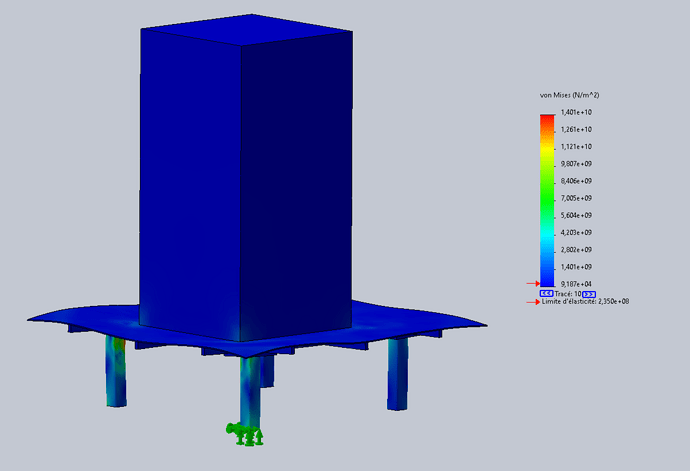
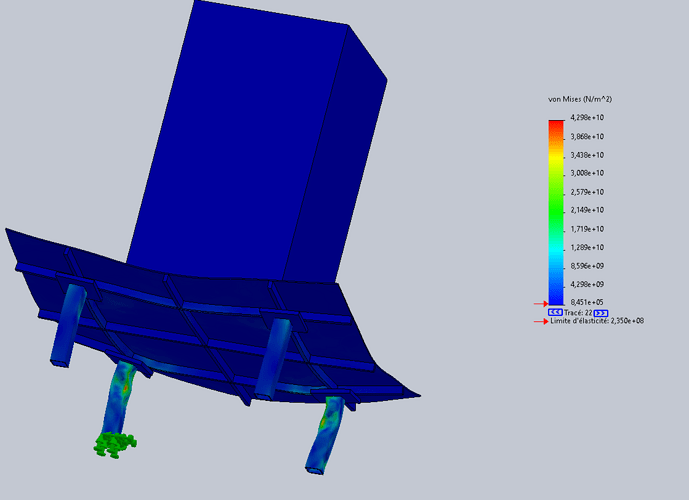
Hallo

Ik heb een klein probleem met de grootte van de structuur en ik zou graag uw verlichte mening willen hebben voordat ik terugkeer.
Ik moet een " tafel " maken (eigenlijk een versterkte plaat met 4 poten) om de val van een massa van 1,1T vanaf een hoogte van 10 meter te ondersteunen.
Mijn probleem is dat ik een waarde van de kinetische energie op het moment van de botsing kan krijgen, in joule, maar Solidworks vraagt me om een waarde in Newton.
Ik begreep dat er een echte test voor nodig was om de vervorming te detecteren en de waarde in N naar voren te brengen, maar dit is voor mij onmogelijk te bereiken.
Is er een " goochelarij " die al bij benadering een waarde van de uit te oefenen kracht aangeeft?
Bedankt
TABEL V2.SLDPRT (283.1 KB)

2

Hallo

Ik heb gekeken op de sites die eenheidsconversie aanbieden en:
1 joule = 1 Nm.

Soms gaan we op zoek naar ingewikkelde...

Vriendelijke groeten.

1 like
3

Hallo
Ja, dat is wat ik had gezien, maar als ik de N's isoleer, moet ik nog steeds de afstand m vinden, die voor mij de vervormde moet zijn (J/m=N). Wat ik niet had... of inderdaad, ik ga te ver zoeken...

4

Hallo

Het is een probleem van afschrijving.
De afstand m hangt precies af van de flexibiliteit van uw tafel, en dus van de vervorming die u kiest om te accepteren.

5

Hallo

Het is een snelle dynamische berekening. Hier is gespecialiseerde software voor (zoals die wordt gebruikt voor auto-crashtests).
Het impactgedrag van materialen kan heel anders zijn dan dat van een quasi-statische trekproef.

6

Ik zou bijvoorbeeld kunnen beginnen met een maximaal aanvaardbare vervorming van 1/300 zoals in structuur? Ik zal een test doen, bedankt

7

Ja, er wordt software aangeboden in 3DXperience, lijkt mij, maar mijn kantoor heeft duidelijk niet de budgetten...

8

Hallo
Aan het einde van een val van 10 m is de kinetische energie van de massa in de orde van grootte van 108e+3 J, energie die moet worden afgevoerd tussen het moment van contact en de immobilisatie van het geheel.
De vraag is: wat zijn de elementen die bijdragen aan deze dissipatie?

We kunnen ons voorstellen dat de " tafel " een stalen constructie is, met een relatief stijf elastisch gedrag.

Maar er wordt niets gespecificeerd over de massa van de val.
Als het een bal pizzadeeg is (een grote, dat geef ik je toe), zal het de mogelijkheid hebben om het grootste deel van de kinetische energie te absorberen door zijn zeer belangrijke elasto-visco-plastische vervorming. Het is een " zachte " schok.
Als het een Twingo (of een Fiat 500) is die van de 3e verdieping van een gebouw is gevallen, zal de vervorming van de auto waarschijnlijk minder groot zijn dan die van het pizzadeeg en zal de tafel zwaarder worden gebruikt.
Als het een stalen bal is, komt het dicht in de buurt van een " harde " schok. De top en de bal zullen de dissipatie moeten delen, met veel hogere krachten dan in de vorige gevallen, vanwege hun respectievelijke aanzienlijke stijfheid.

Er kan een eenvoudig dynamisch model worden ontwikkeld, gebaseerd op een contactinterface bestaande uit veren en dempers. De moeilijkheid ligt in het geven van waarden aan hun stijfheid en dempingsfactoren.
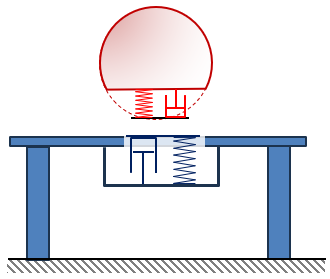
image

We zouden meer moeten weten over de aard en structuur van de tafel en de bewegende massa, om te proberen deze coëfficiënten te schatten...
Vriendelijke groeten.

7 likes
9

Hallo

Het lijkt erop dat het mogelijk is om een simulatie van uw probleem rechtstreeks op solidworks uit te voeren.
Alleen verkrijgbaar vanaf een professionele simulatielicentie in ieder geval.

1 like
10

Hallo, we hebben de Premium- en pro-simulatie, maar het enige dat ze bieden is een simulatie van het object dat zelf op een vloer valt die niet wordt geanalyseerd. Wat mij interesseert is de val van een object op mijn object van analyse.

11

Als ik me niet vergis, kun je, zodra de analyse van de val is voltooid, met de rechtermuisknop klikken op "Beperken" onder Resultaat en de tool "Probe" selecteren.

Op die manier kunt u de maximale beperking zien.

Met deze maximale beperking kunt u een statische simulatie opnieuw uitvoeren.

Ik heb alleen de standaard simulatiemodule, ik kon helemaal niet verifiëren wat ik je vertel!
(maar zo zou ik het gedaan hebben)

12

Hier gaat het erom te zien hoe mijn structuur reageert op de impact van een kiezelsteen van een ton, niet hoe mijn structuur reageert als deze valt.
Zoals gewoonlijk wordt mij gevraagd om een bouwwerk te controleren dat al haastig is gebouwd... Ik betwijfel of het helemaal niet werkt, maar ik wil toch een betrouwbaar resultaat kunnen leveren, en zelfs weten hoe ik het moet doen voor mijn professionele cultuur...
Ik heb het TQC-gedeelte in PJ in mijn eerste post gezet

13

Hallo
Ik heb de munt in PJ in mijn 1e post gezet.
Wat betreft de massa die inslaat, het is ijzererts. Er kan van worden uitgegaan dat het voldoende geagglomereerd is om niet te vervormen bij een botsing...

14

Ik vond dit als het je kan helpen:

15

Ja! Ik zal er meteen :wink: naar kijken, bedankt

16

Op zich is het juist de relatieve beweging die wordt omgekeerd.
Ik weet niet hoe ik dit soort onderzoek naar SW moet opzetten, maar om de tafel met voldoende snelheid te laten vallen om een equivalente kinetische energie te hebben?

17

Ja, ik heb erover nagedacht, ik zal het zo snel mogelijk :wink: proberen Dank je

18

Ja, maar de inspanning zal op de voeten zijn en niet op het werkblad?

19

Hallo
Heeft u meer informatie over het formulier... van uw object dat in botsing komt met uw reeds berekende tabel?
Ik heb een vereenvoudigde vorm gemaakt om de massa van een ton te hebben, ik heb een sectie van 0,26 m², de hoogte die compatibel is, krijg ik met de dichtheid. S235 basis voor uw tafel en voor het projectiel.

De door u opgegeven waarden: een massa van 1,1 ton (1100 kg) en een valhoogte van 10 meter.

Laten we eerst de snelheid op het moment van de inslag berekenen met behulp van de formule voor het behoud van mechanische energie:

m * g * h = (1/2) * m * v^2

waarbij m de massa (1100 kg) is, g de versnelling door de zwaartekracht (9,8 m/s^2) en h de valhoogte (10 meter).

1100 kg * 9,8 m/s^2 * 10 m = (1/2) * 1100 kg * v^2

107800 J = 550 v^2

Als we deze vergelijking oplossen, kunnen we de waarde van de snelheid v vinden:

v^2 = 107800 J / 550 kg v^2 ≈ 196,18 m^2/s^2 v ≈ √196,18 m/s v ≈ 14 m/s

Ik ben het eens met de joules van het vorige antwoord.
En op het eerste gezicht zijn het de voeten die het eerste probleem zijn...

image
afbeelding1203×822 82.6 KB

Spectrum.

P.S/

Drop Tijd = √(2*Hoogte/g)

waarbij hoogte de hoogte van de val is (10 meter) en g de versnelling door de zwaartekracht (ongeveer 9,8 m/s^2).

Als we de waarden in de formule plaatsen, krijgen we:

Valtijd = √(2 * 10 m / 9.8 m/s^2) Valtijd ≈ √(2.04 s^2) Valtijd≈ 1.43 s

De duur van de val van het object is dus ongeveer 1,43 seconden.

image
afbeelding1119×812 103 KB

2 likes
20

Het is niet verkeerd...