Problem z wymiarowaniem udarów między częściami

Out of category
,
1

Witam

Mam mały problem z wymiarem konstrukcji i chciałbym poznać Wasze oświecone opinie przed dokonaniem zwrotu.
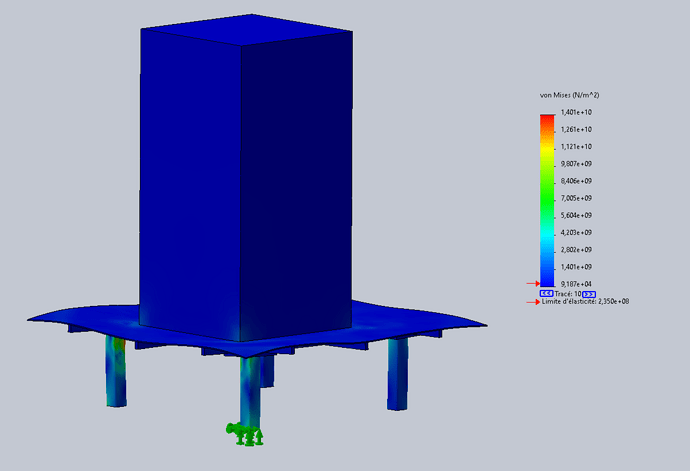
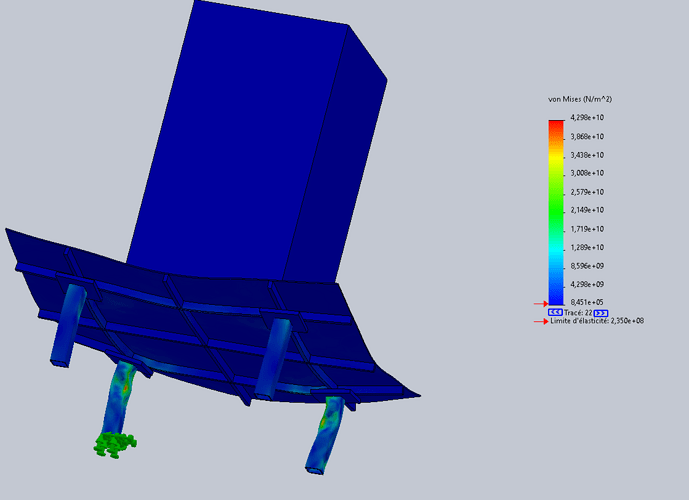
Muszę zrobić " stół " (w zasadzie wzmocnioną płytę z 4 nogami) do podtrzymania upadku masy 1,1T z wysokości 10 metrów.
Mój problem polega na tym, że mogę uzyskać wartość energii kinetycznej w momencie uderzenia, w dżulach, ale Solidworks prosi mnie o wartość w niutonach.
Zrozumiałem, że potrzeba prawdziwego testu, aby wykryć odkształcenie i wydobyć wartość w N, ale jest to dla mnie niemożliwe do osiągnięcia.
Czy istnieje " kuglarstwo ", które już określa przybliżoną wartość siły, która ma być przyłożona?
Dziękuję
TABELA V2.SLDPRT (283.1 KB)

2

Witam

Spojrzałem na strony, które oferują konwersję jednostek i:
1 dżul = 1 Nm.

Czasami szukamy skomplikowanych...

Pozdrowienia.

1 polubienie
3

Witam
Tak, to jest to, co widziałem, ale jeśli wyizoluję N, to i tak muszę znaleźć odległość m, która musi być dla mnie zdeformowana (J/m=N). Czego nie miałem... a właściwie zamierzam szukać za daleko...

4

Witam

To problem deprecjacji.
Odległość m zależy dokładnie od elastyczności stołu, a tym samym od odkształcenia, które zdecydujesz się zaakceptować.

5

Witam

To szybka dynamiczna kalkulacja. Istnieje do tego specjalistyczne oprogramowanie (takie jak te używane do testów zderzeniowych samochodów).
Zachowanie materiałów podczas uderzenia może być zupełnie inne niż w przypadku quasi-statycznej próby rozciągania.

6

Na przykład, mógłbym zacząć od maksymalnego dopuszczalnego odkształcenia 1/300, jak w strukturze? Zrobię test, dziękuję

7

Wydaje mi się, że tak, oprogramowanie jest oferowane w 3DXperience, ale moje biuro oczywiście nie ma budżetów...

8

Witam
Pod koniec upadku z wysokości 10 m energia kinetyczna masy jest rzędu 108e+3 J, energia, która musi zostać rozproszona między momentem zetknięcia się a unieruchomieniem całości.
Pytanie brzmi: jakie są elementy, które przyczyniają się do tego rozproszenia?

Możemy sobie wyobrazić, że " stół " jest konstrukcją stalową, o stosunkowo sztywnym zachowaniu sprężystym.

Ale nic nie jest sprecyzowane na temat masy upadku.
Jeśli jest to kulka ciasta na pizzę (duża, przyznaję wam), będzie miała zdolność pochłaniania większości energii kinetycznej poprzez swoje bardzo ważne odkształcenie elasto-lepkościowo-plastyczne. Jest to " miękki " wstrząs.
Jeśli jest to Twingo (lub Fiat 500) upuszczony z 3 piętra budynku, odkształcenie samochodu będzie prawdopodobnie mniej znaczące niż odkształcenia ciasta na pizzę, a stół będzie bardziej obciążony.
Jeśli jest to stalowa kula, jest to bliskie " twardemu " wstrząsowi. Góra i piłka będą musiały dzielić się rozpraszaniem, ze znacznie większymi siłami niż w poprzednich przypadkach, ze względu na ich znaczną sztywność.

Można opracować prosty model dynamiczny, oparty na interfejsie kontaktowym składającym się ze sprężyn i amortyzatorów. Trudność polega na podaniu wartości ich sztywności i współczynników tłumienia.
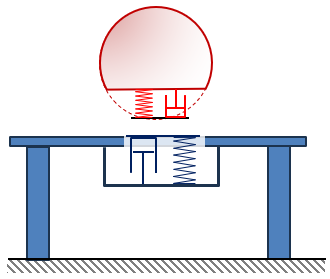
image

Musielibyśmy wiedzieć więcej o naturze i strukturze tabeli oraz poruszającej się masie, aby spróbować oszacować te współczynniki...
Pozdrowienia.

7 polubień
9

Witam

Wygląda na to, że możliwe jest przeprowadzenie symulacji problemu bezpośrednio w solidworks.
Dostępne tylko z licencją na profesjonalną symulację.

1 polubienie
10

Witam, mamy symulację Premium i pro, ale jedyne, co oferują, to symulacja obiektu spadającego sama na podłogę, która nie jest analizowana. To, co mnie interesuje, to upadek przedmiotu na mój przedmiot analizy.

11

Jeśli się nie mylę, po zakończeniu analizy spadku możesz kliknąć prawym przyciskiem myszy na "Ograniczenie" w sekcji Wynik i wybrać narzędzie "Sonda".

W ten sposób możesz zobaczyć ograniczenie max.

Za pomocą tego maksymalnego ograniczenia można ponownie wykonać symulację statyczną.

Mam tylko standardowy moduł symulacji, w ogóle nie mogłem zweryfikować tego, co mówię!
(ale ja bym tak to zrobił)

12

Tutaj chodzi o to, aby zobaczyć, jak moja konstrukcja reaguje na uderzenie jednotonowego kamyka, a nie jak moja konstrukcja reaguje, gdy upada.
Jak zwykle jestem proszony o sprawdzenie konstrukcji, która została już zbudowana w pośpiechu... Wątpię, że to w ogóle nie działa, ale nadal chcę być w stanie dostarczyć wiarygodny wynik, a nawet wiedzieć, jak to zrobić dla mojej kultury zawodowej...
Część TQC w PJ umieściłem w moim pierwszym poście

13

Witam
Monetę włożyłem w piżamę w moim 1 poście.
Jeśli chodzi o masę, która uderza, jest to ruda żelaza. Można uznać, że jest wystarczająco aglomerowany, aby nie odkształcać się przy uderzeniu...

14

Znalazłem to, jeśli może ci pomóc:

15

Tak! Przyjrzę się temu od razu :wink: , dziękuję

16

Sam w sobie jest to po prostu względny ruch, który jest odwrócony.
Nie wiem, jak zorganizować tego rodzaju badanie na SW, ale tak, aby stół opadał z wystarczającą prędkością, aby miał równoważną energię kinetyczną?

17

Tak, myślałem o tym, spróbuję tak szybko, jak to możliwe :wink: Dziękuję

18

Tak, ale wysiłek będzie leżał na nogach, a nie na blacie?

19

Witam
Czy masz więcej informacji na temat formularza... Twojego obiektu, który będzie kolidował z już obliczoną tabelą?
Zrobiłem uproszczony kształt, aby mieć masę jednej tony, mam przekrój 0,26 m², wysokość kompatybilna z gęstością otrzymuję ją z gęstością. Podstawa S235 do twojego stołu i do pocisku.

Podane przez Ciebie wartości: masa 1,1 tony (1100 kg) i wysokość upadku 10 metrów.

Najpierw obliczmy prędkość w momencie uderzenia, korzystając ze wzoru na zachowanie energii mechanicznej:

m * g * h = (1/2) * m * v^2

gdzie m to masa (1100 kg), g to przyspieszenie ziemskie (9,8 m/s^2), a h to wysokość upadku (10 metrów).

1100 kg * 9,8 m/s^2 * 10 m = (1/2) * 1100 kg * v^2

107800 J = 550 v^2

Rozwiązując to równanie, możemy znaleźć wartość prędkości v:

v^2 = 107800 J / 550 kg v^2 ≈ 196,18 m^2/s^2 v ≈ √196,18 m/s v ≈ 14 m/s

Zgadzam się z dżulami poprzedniej odpowiedzi.
I na pierwszy rzut oka to stopy są pierwszym problemem...

image
obraz1203×822 82.6 KB

Widmo.

P.S/

Czas upuszczania = √(2*Wysokość/g)

gdzie wysokość to wysokość upadku (10 metrów), a g to przyspieszenie grawitacyjne (około 9,8 m/s^2).

Podstawiając wartości do wzoru, otrzymujemy:

Czas upadku = √(2 * 10 m / 9.8 m/s^2) Czas upadku ≈ √(2.04 s^2) Czas upadku≈ 1.43 s

Tak więc czas upadku obiektu wynosi około 1,43 sekundy.

image
obraz1119×812 103 KB

2 polubienia
20

To nie jest złe...