Bonjour,
Je voudrais concevoir une spirale dont la section est progressive du centre à l’extérieur comme sur l’image?
merci
Diiity

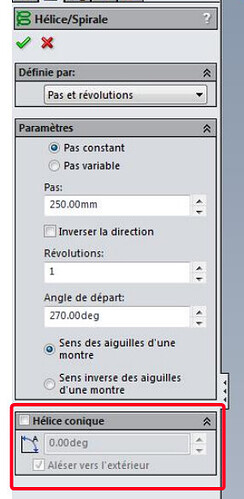
Regarde ce tuto pour faire des spires:
https://mycad.visiativ.com/en/node/788960
Pour la spire conique il suffit de cocher cette case en +:
Même si il date un peu il est toujours fonctionnel.
Oups à plat voir ce tuto:
Merci les gars, j’arrive à la faire mais la section est constante tout le long alors que je voudrai qu’elle s’évase progressivement par exemple de 10mm au centre à 30mm à l’extérieur.
Bonjour,
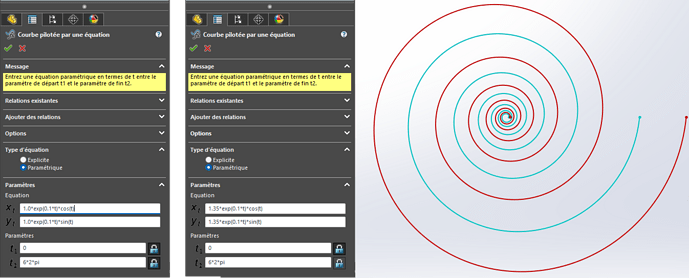
Vos spirales ressemblent à des spirales logarithmiques, dont les équations paramétriques cartésiennes sont les suivantes, avec a et b constantes :
![]()
Une première spirale est tracée dans une esquisse, par la fonction « Outils > Entités d’esquisse > Courbe pilotée par une équation », avec les valeurs a = 1.0 et b = 0.1 :
![]()
Pour t compris entre 0 et 6x2xpi (de 0 à 6 tours)
Une seconde esquisse contient une seconde spirale en faisant varier légèrement le paramètre a (a = 1.35):
![]()
Toujours avec t compris entre 0 et 6x2xpi (de 0 à 6 tours).
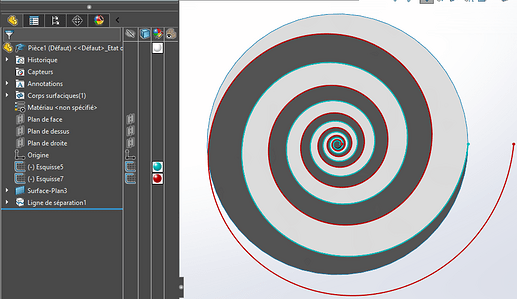
Ce qui donne le résultat suivant :
Une troisième esquisse reprend les spirales, définit le bord et le centre du disque, et le tour est joué avec une surface et une ligne de séparation.
Il est possible de tout faire avec une seule esquisse, mais il n’y a pas l’agrément de la couleur pour bien distinguer les deux spirales.
Modèle SW 2022 ci-dessous, à adapter en jouant sur les valeurs des coefficients a et b.
Spirales.SLDPRT (144,2 Ko)
Super ça marche.
Par contre, comment fait on pour revoir les formules et les corriger si cela ne convienst pas?
Le modèle joint utilise les équations de Solidworks pour paramétrer les spirales:
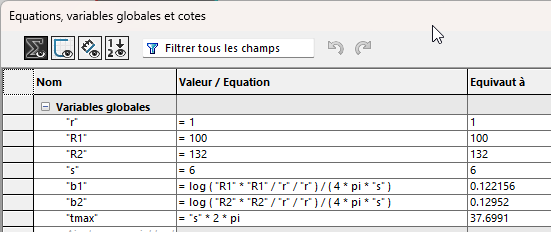
- r : rayon intérieur (aucune raison de le modifier…) ;
- R1 : rayon extérieur de la spirale n°1. C’est aussi le rayon extérieur du disque ;
- R2: : rayon extérieur de la spirale n°2. Doit être supérieur à R1 ;
- s : nombre de tours, identique pour les deux spirales ;
- b1 et b2 : coefficients des équations des spirales, calculés en fonction des variables précédentes ;
- tmax : valeur maxi du paramètre pour les équations.
Définir dans l’ordre s, puis R1 qui est le diamètre extérieur du disque. La spirale n°1 est ainsi complètement définie.
Entrer ensuite R2, supérieur à R1. Un trop gros écart entre les deux rayons peut provoquer une erreur dans la suite de la construction. Il faut faire progresser R2 avec prudence…
Il faut sortir du module d’équations pour reconstruire. Une reconstruction simple (Ctrl B) ne suffit pas, il faut une reconstruction forcée (Ctrl Q) pour regénérer la géométrie.
Les équations des spirales utilisant les variables sont parfois instables (borne « tmax » remplacée par une valeur numérique ???). Dans cette situation, il faut ressaisir l’expression.
Spirales.SLDPRT (139,1 Ko)
bien merci