Witam
Chciałbym zaprojektować spiralę, której przekrój jest progresywny od środka na zewnątrz jak na zdjęciu?
Dziękuję
Odrębność

Zapoznaj się z tym samouczkiem, aby wykonać skręty:
https://mycad.visiativ.com/en/node/788960
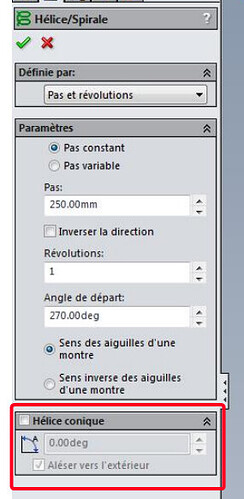
W przypadku cewki stożkowej wystarczy zaznaczyć to pole w +:
Nawet jeśli jest trochę przestarzały, nadal działa.
Ups płaskie, zobacz ten samouczek:
Dzięki chłopaki, mogę to zrobić, ale przekrój jest cały czas stały, podczas gdy chciałbym, aby stopniowo się rozszerzał, na przykład od 10 mm w środku do 30 mm na zewnątrz.
Witam
Twoje spirale wyglądają jak spirale logarytmiczne, których kartezjańskie równania parametryczne są następujące, ze stałymi a i b:
![]()
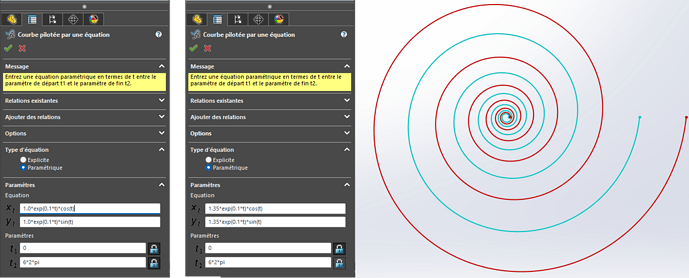
Pierwsza spirala jest rysowana w szkicu za pomocą funkcji " Narzędzia > elementów szkicu >Krzywa sterowana równaniem ", z wartościami a = 1,0 i b = 0,1:
![]()
Dla t od 0 do 6x2xpi (od 0 do 6 obrotów)
Drugi szkic zawiera drugą spiralę poprzez nieznaczną zmianę parametru a (a = 1,35):
![]()
Zawsze z t od 0 do 6x2xpi (od 0 do 6 zwojów).
Daje to następujący wynik:
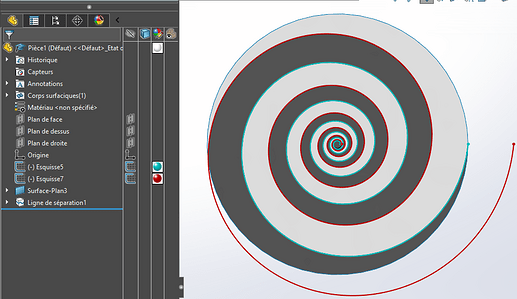
Trzeci szkic obejmuje spirale, określa krawędź i środek dysku, a to wszystko z powierzchnią i linią podziału.
Możliwe jest zrobienie wszystkiego za pomocą jednego szkicu, ale nie ma przyjemności z koloru, aby odróżnić dwie spirale.
Model SW 2022 poniżej, do dostosowania poprzez zabawę wartościami współczynników a i b.
Spirale.SLDPRT (144.2 KB)
Świetnie, to działa.
Z drugiej strony, w jaki sposób możemy przejrzeć formuły i je poprawić, jeśli nie są odpowiednie?
Załączony model wykorzystuje równania Solidworks do parametryzacji krzywych:
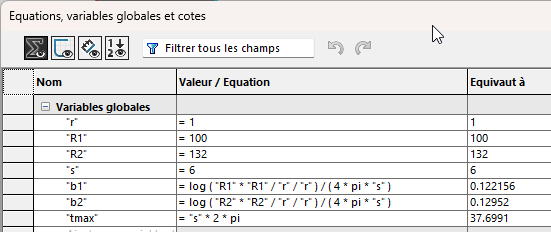
- R: Promień wewnętrzny (nie ma powodu, aby go zmieniać...);
- R1: promień zewnętrzny spirali nr 1. Jest to również zewnętrzny promień dysku;
- R2: : promień zewnętrzny spirali nr 2. Musi być większa niż R1;
- s : liczba obrotów, identyczna dla obu spiral ;
- b1 i b2: współczynniki równań spiralnych, obliczone zgodnie z poprzednimi zmiennymi;
- tmax: maksymalna wartość parametru równań.
Zdefiniuj w kolejności s, a następnie R1, która jest zewnętrzną średnicą dysku. Spirala nr 1 jest w ten sposób całkowicie zdefiniowana.
Następnie wprowadź wartość R2, większą niż R1. Zbyt duża szczelina między dwoma szprychami może spowodować błąd w dalszej konstrukcji. Musimy postępować z R2 ostrożnie...
Musimy wyjść z modułu równania, aby odbudować. Prosta rekonstrukcja (Ctrl B) nie wystarczy, do regeneracji geometrii potrzebna jest rekonstrukcja wymuszona (Ctrl Q).
Równania spiral wykorzystujące zmienne są czasami niestabilne (granica " tmax " zastąpiona wartością liczbową ???). W tej sytuacji musimy ponownie uchwycić ten wyraz.
Spirals.SLDPRT (139.1 KB)
Piękne dzięki