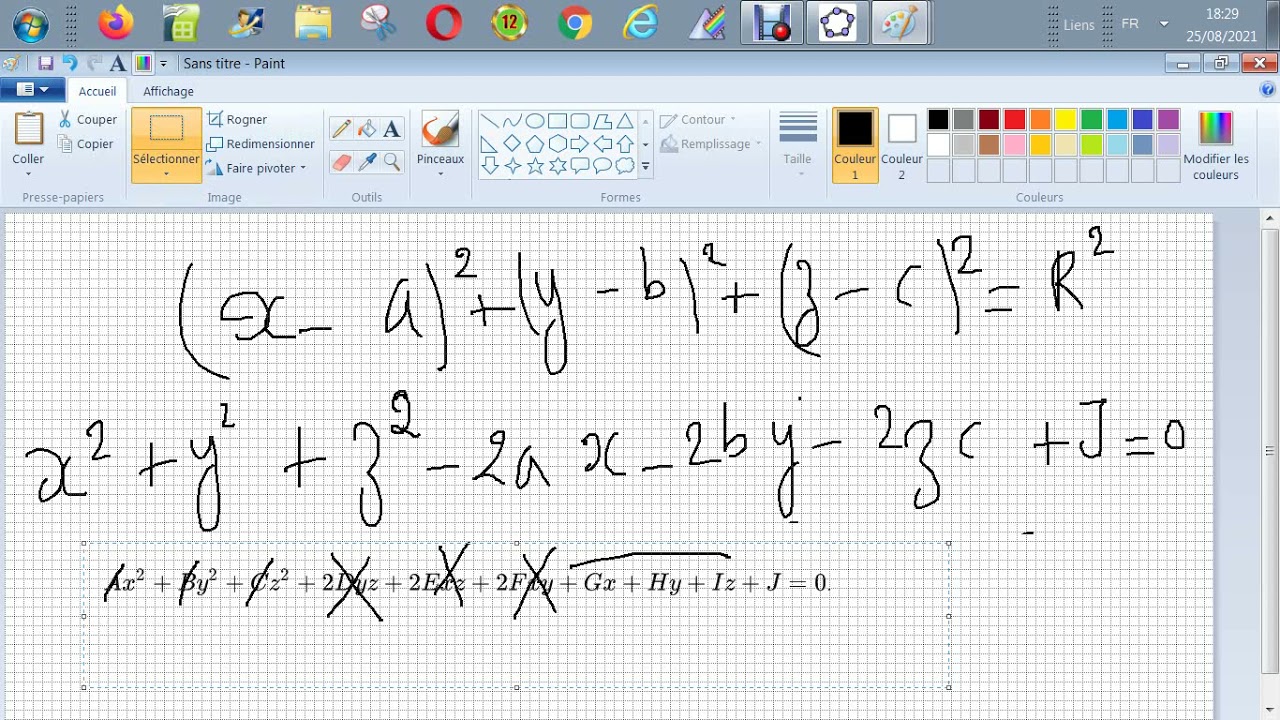Ich versuche, eine sphärische Oberfläche zu bauen, die durch 4 bekannte Punkte im Raum verläuft. Es scheint mir, dass ich wusste, wie man es auf Catia macht... Was ist mit SW.
Vielen Dank für Ihre Antwort.
Schon wenn es sich um eine Kugel handelt, reichen 3 Punkte.
Hallo
Ich sehe keine einfache Methode oder Funktion, um dies zu tun.
Mit den 4 Punkten mache ich ein Volumen, aus dem ich den Schwerpunkt erhalte.
Von diesem Punkt und zwei der Anfangspunkte aus werde ich einen Plan und dann eine Skizze erstellen, um die Kugel mit einer Umdrehung herzustellen
Man kann nicht wirklich 
einen Kreis machen, sondern eine Unendlichkeit von Kugeln
Es sei denn, der Mittelpunkt ist einer der Punkte. Und wieder mit einer Mitte brauchst du nur 2 Punkte
Und ja, aber es handelt sich um eine Kugel, die durch 4 Punkte geht 
Eine andere Methode (vielleicht, da ich nicht hellwach 
bin):
Fixpunkte an den gewünschten Koordinaten in einer 3D-Skizze,
Eine Volumenkugel aus einer 3D-Skizze mit einem pilotierten Radius,
Fügen Sie Tangentialabhängigkeiten zwischen der Fläche und den Punkten hinzu.
In Ermangelung einer schnellen Methode in SW, vielleicht mit dieser Methode:
Ich für meinen Teil habe nicht alles geschaut, es ist Montagmorgen!
Durch die vier nicht-koplanaren Punkte A, B, C und D durchläuft es eine einzige Kugel.
Tatsächlich habe ich ein Polyeder, dessen Ecken durch Parametrisierung definiert sind, es ist in eine Kugel eingeschrieben, deren Zentrum ich sammeln möchte...
1 „Gefällt mir“
Ich möchte SW nicht verlassen... mit einer Gleichung, mit der man umgehen muss!
1 „Gefällt mir“
Hallo
Du nimmst die ersten 3 Punkte: A, B und C, → du eine Ebene erstellst, die durch die 3 Punkte verläuft, und du erstellst den Kreis, der durch diese 3 Punkte verläuft, → du einen Mittelpunkt hast, → zeichnest du die Senkrechte zu der Ebene, die durch den Mittelpunkt verläuft.
Du nimmst D, C und D (oder besser B, wie @Sylk gesagt hast), du machst das Gleiche → zweiten Geraden senkrecht zur zweiten Ebene
Schnittpunkt der 2 Linien → Mittelpunkt der Kugel (wenn SW es zulässt, dass Sie sie mit den Kurven erstellen...)
Kugel 4 Punkte. SLDPRT (138.3 KB)
Hinweis: Es hat mit dem in V2020 angehängten Beispiel funktioniert
3 „Gefällt mir“
Du meintest B, C und D
1 „Gefällt mir“
Das ist nicht falsch 
2 „Gefällt mir“
Ein schwieriger Start in den Montag für viele Menschen offensichtlich
2 „Gefällt mir“
Ich bin beeindruckt!
2 „Gefällt mir“
Hallo
Eine andere Lösung...
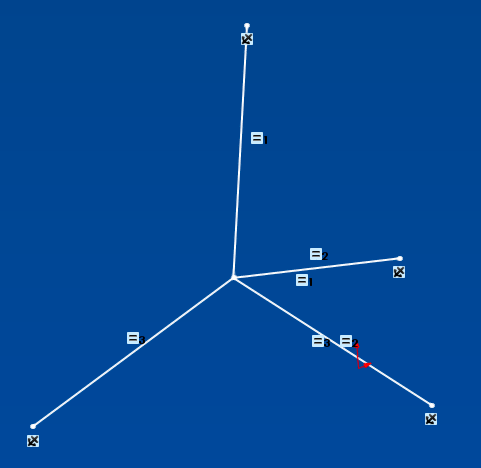
Zeichnen Sie in einer 3D-Skizze 4 Segmente von einem beliebigen unbeschränkten Punkt P zu den 4 Punkten A, B, C und D. Fügen Sie eine Gleichheitsbeziehung auf den Längen der 4 Segmente hinzu, und Sie sind fertig. P ist der Mittelpunkt der Kugel.
3 „Gefällt mir“
Ja... Ich werde versuchen!
Deutlich einfacher zu bauen als das, was ich vorgeschlagen habe (aber ich kann spüren, dass SW bei Änderungen ziemlich schnell überall rot wird).
1 „Gefällt mir“
Ja, es wird von Anfang an rot (unmöglich, die Gleichheit bei den 4 Segmenten zu setzen - > bei direkter Einschränkung)
Es funktioniert sehr gut. Sie müssen nur die nützlichen Beziehungen einfügen:
- alle automatischen Beziehungen zu löschen, die nach der Erstellung der Segmente bestehen (z. B. Koinzidenzen oder Rechtwinkligkeiten),
- Fügen Sie jedem Segmentendpunkt eine feste Beziehung hinzu (da die Koordinaten bekannt und fest sind),
- Markieren Sie alle Zeilen in den Segmenten und fügen Sie eine Gleichheitsbeziehung hinzu.
Bitte schön.
1 „Gefällt mir“