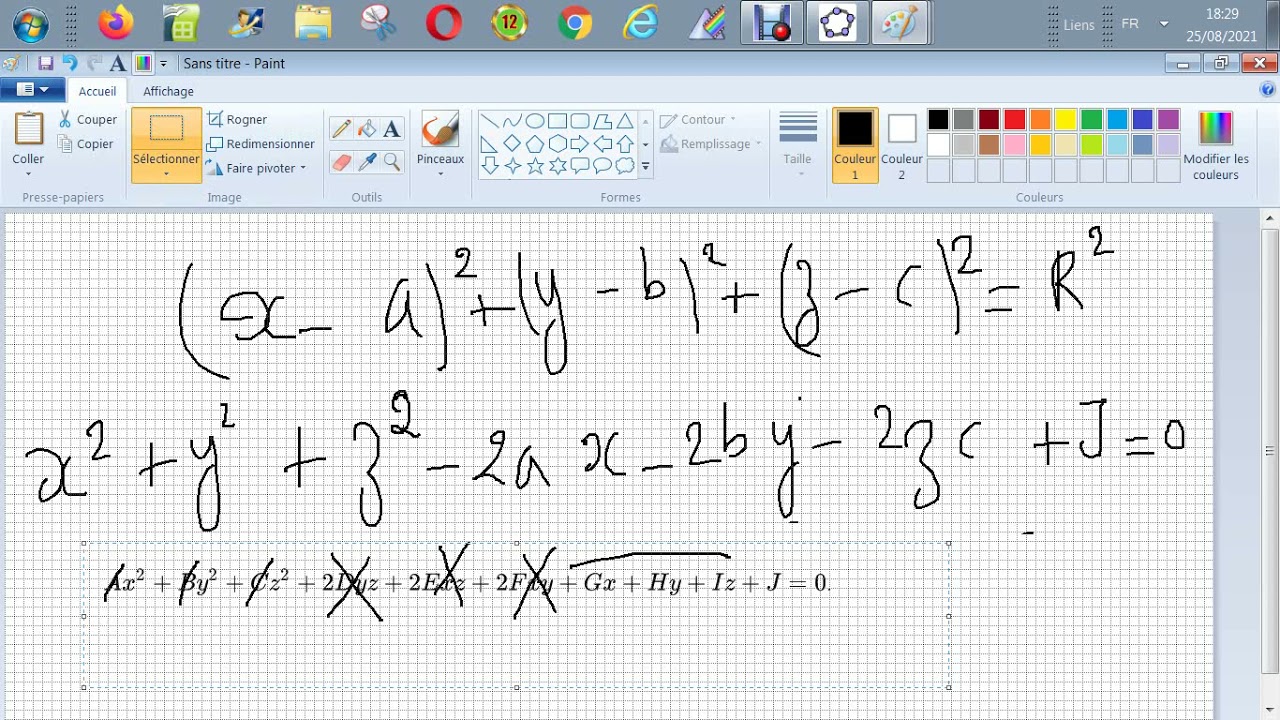Spherical surface passing through 4 known points in space

3D Design Surface Modeling
1

I am trying to build a spherical surface passing through 4 known points in space. It seems to me that I knew how to do it on Catia... What about SW.
Thank you for your answer.

2

Already if it's a sphere, 3 points are enough.

3

Hello

I don't see a simple method or function to do this.

With the 4 points I will make a volume from which I will obtain the center of mass.
From this point and two of the initial points, I will make a plan and then a sketch to make the sphere with one revolution

4

not really :slight_smile: you can make a circle but an infinity of spheres

5

Unless the center is one of the points. And again with a center you only need 2 points

6

And yes, but the question concerns a sphere passing through 4 points :wink:

7

Another method (maybe, since I'm not wide awake :sweat_smile:):

Fixed points at the desired coordinates in a 3D sketch,
A volume sphere from a 3D sketch with a piloted radius,
Add tangency constraints between the surface and the points.

8

In the absence of a quick method in SW, perhaps with this method:

For my part, I didn't watch everything, it's Monday morning!

9

Through four non-coplanar points A, B, C and D, it passes through a single sphere.

In fact, I have a polyhedron whose corners are defined by parameterization, it is inscribed in a sphere whose center I want to collect...

1 Like
10

I would like not to leave SW... with an equation to deal with!

1 Like
11

Hello
You take the first 3 points: A, B and C → you make a plane passing through the 3 points and you create the circle passing through these 3 points → you have a center → you draw the perpendicular to the plane passing through the center.

You take D, C and D (or rather B as @Sylk pointed out), you do the same → second straight line perpendicular to the second plane

Intersection of the 2 lines → center of the sphere (if SW allows you to create it with the curves...)

sphere 4 points. SLDPRT (138.3 KB)

Nb: it worked with the example attached in V2020

3 Likes
12

You meant B, C and D

1 Like
13

It's not wrong :stuck_out_tongue_winking_eye:

2 Likes
14

A difficult start to Monday for many people obviously :sweat_smile:

2 Likes
15

So I'm impressed!

2 Likes
16

Hello

Another solution...
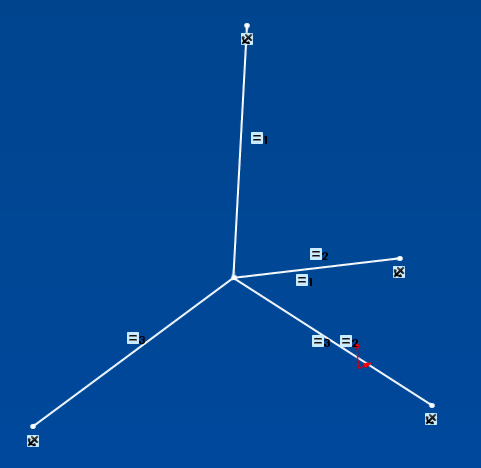
In a 3D sketch, draw 4 segments from any unconstrained point P to the 4 points A, B, C, and D. Add an equality relationship on the lengths of the 4 segments, and you're done. P is the center of the sphere.

3 Likes
17

Yes... I will try!

18

Significantly easier to build than what I proposed (but I can feel SW putting red everywhere quite quickly in case of modifications).

1 Like
19

Yes, it goes red from the beginning (impossible to put the equality at the 4 segments-> on direct constraint)

20

It works very well. You just have to put only the useful relationships:

  • delete any automatic relationship that exists after the creation of the segments (such as coincidences or perpendicularities),
  • add a Fixed relationship to each segment endpoint (since the coordinates are known and fixed),
  • Select all the rows in the segments and add an equality relationship.
    There you go.

image

1 Like