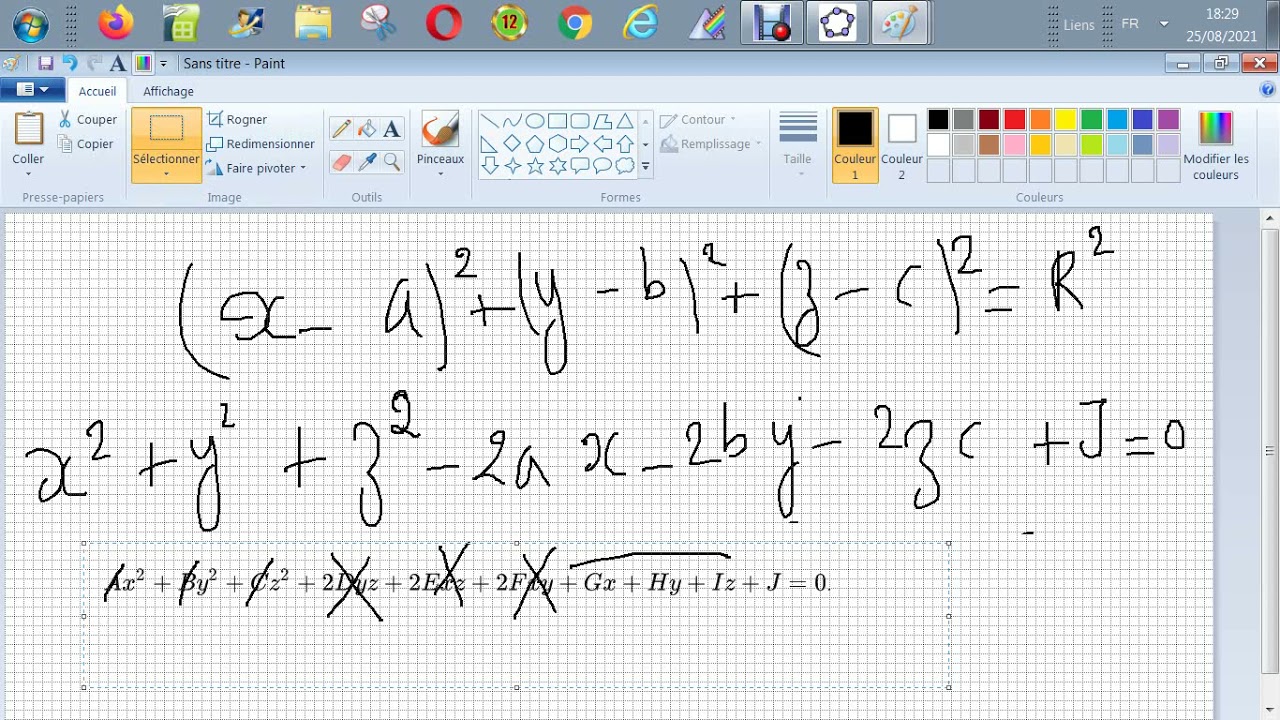Ik probeer een bolvormig oppervlak te bouwen dat door 4 bekende punten in de ruimte loopt. Het lijkt mij dat ik wist hoe ik het op Catia moest doen... Hoe zit het met SW.
Dank u voor uw antwoord.
Al als het een bol is, zijn 3 punten genoeg.
Hallo
Ik zie geen eenvoudige methode of functie om dit te doen.
Met de 4 punten ga ik een boek maken waaruit ik het zwaartepunt zal halen.
Vanaf dit punt en twee van de eerste punten zal ik een plan maken en vervolgens een schets om de bol met één omwenteling te maken
Niet echt 
kun je een cirkel maken, maar een oneindig aantal bollen
Tenzij het centrum een van de punten is. En nogmaals, met een centrum heb je maar 2 punten nodig
En ja, maar de vraag betreft een bol die door 4 punten gaat 
Een andere methode (misschien, aangezien ik niet klaarwakker 
ben):
Vaste punten op de gewenste coördinaten in een 3D-schets,
Een volumebol uit een 3D-schets met een bestuurde radius,
Voeg tangentiebeperkingen toe tussen het oppervlak en de punten.
Bij gebrek aan een snelle methode in SW, misschien met deze methode:
Van mijn kant heb ik niet alles bekeken, het is maandagochtend!
Door vier niet-coplanaire punten A, B, C en D gaat het door een enkele bol.
In feite heb ik een veelvlak waarvan de hoeken worden bepaald door parametrisering, het is gegraveerd in een bol waarvan ik het centrum wil verzamelen...
1 like
Ik wil SW niet verlaten... met een vergelijking om mee om te gaan!
1 like
Hallo
Je neemt de eerste 3 punten: A, B en C → je maakt een vlak dat door de 3 punten gaat en je maakt de cirkel die door deze 3 punten gaat → je hebt een centrum → je tekent de loodlijn op het vlak dat door het centrum gaat.
Je neemt D, C en D (of liever B zoals @Sylk aangegeven), je doet hetzelfde → tweede rechte lijn loodrecht op het tweede vlak
Kruising van de 2 lijnen → midden van de bol (als SW het toestaat om het te creëren met de rondingen...)
bol 4 punten. SLDPRT (138.3 KB)
Nb: het werkte met het voorbeeld dat in V2020 was bijgevoegd
3 likes
Je bedoelde B, C en D
1 like
Het is niet verkeerd 
2 likes
Een moeilijke start van maandag voor veel mensen natuurlijk
2 likes
Dus ik ben onder de indruk!
2 likes
Hallo
Een andere oplossing...
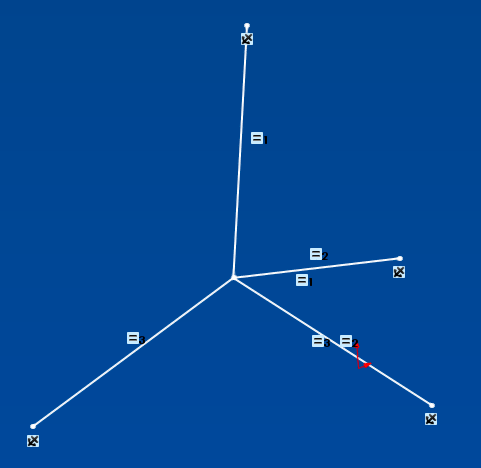
Teken in een 3D-schets 4 segmenten van elk onbeperkt punt P naar de 4 punten A, B, C en D. Voeg een gelijkheidsrelatie toe aan de lengtes van de 4 segmenten en je bent klaar. P is het centrum van de bol.
3 likes
Ja... Ik zal proberen!
Aanzienlijk gemakkelijker te bouwen dan wat ik had voorgesteld (maar ik voel dat SW vrij snel overal rood zet in geval van wijzigingen).
1 like
Ja, het wordt vanaf het begin rood (onmogelijk om de gelijkheid op de 4 segmenten-> op directe beperking te zetten)
Het werkt heel goed. Je hoeft alleen maar alleen de nuttige relaties te plaatsen:
- verwijder alle automatische relaties die bestaan na het maken van de segmenten (zoals toevalligheden of loodlijnen),
- voeg een vaste relatie toe aan elk segmenteindpunt (aangezien de coördinaten bekend en vast zijn),
- Selecteer alle rijen in de segmenten en voeg een gelijkwaardigheidsrelatie toe.
Daar ga je.
1 like