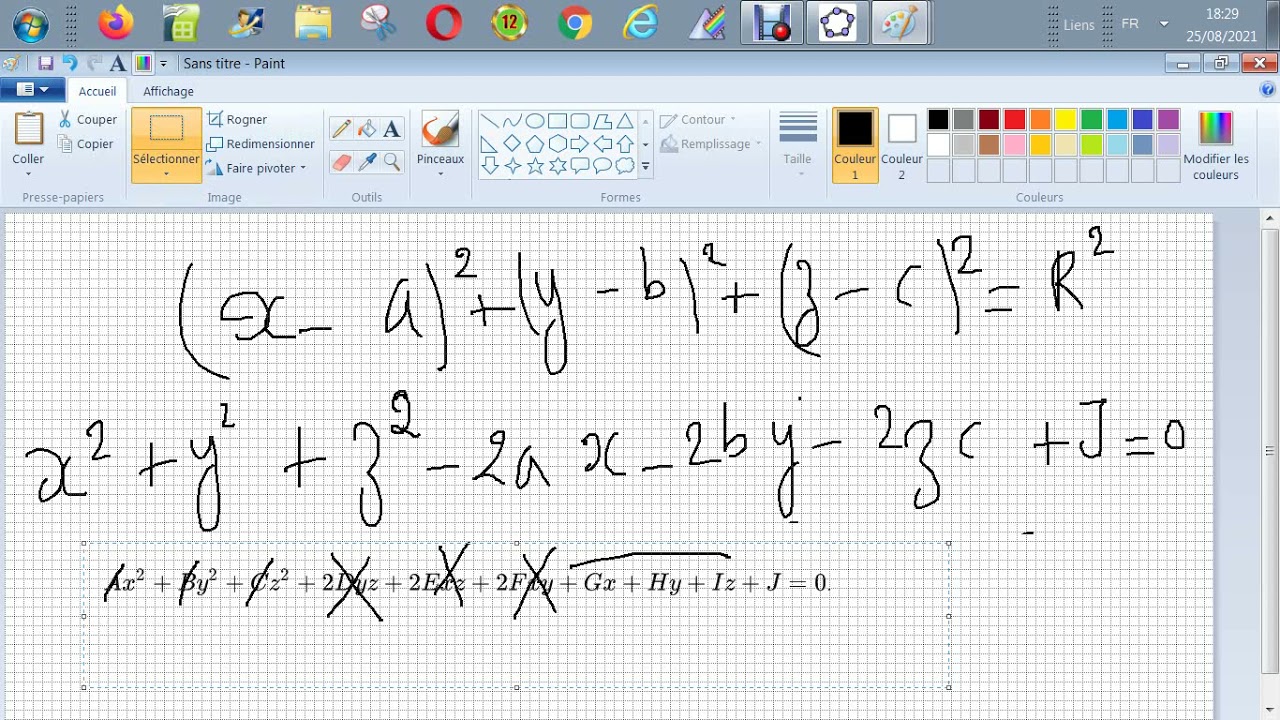Próbuję zbudować sferyczną powierzchnię przechodzącą przez 4 znane punkty w przestrzeni. Wydaje mi się, że wiedziałem, jak to zrobić na Catii... A co z SW.
Dziękuję za odpowiedź.
Już jeśli jest to kula, wystarczą 3 punkty.
Witam
Nie widzę prostej metody ani funkcji, aby to zrobić.
Z 4 punktów stworzę objętość, z której uzyskam środek masy.
Z tego punktu i dwóch początkowych punktów wykonam plan, a następnie szkic, aby wykonać kulę za pomocą jednego obrotu
Tak naprawdę 
nie możesz zrobić koła, ale nieskończoność sfer
Chyba, że środek jest jednym z punktów. I znowu z centrum potrzebujesz tylko 2 punktów
I tak, ale pytanie dotyczy kuli przechodzącej przez 4 punkty 
Inna metoda (być może, ponieważ nie jestem całkowicie rozbudzony 
):
Stałe punkty na żądanych współrzędnych w szkicu 3D,
Sfera objętościowa ze szkicu 3D z pilotowanym promieniem,
Dodać wiązania styczności między powierzchnią a punktami.
W przypadku braku szybkiej metody w SW, być może z tą metodą:
Ze swojej strony nie obejrzałem wszystkiego, jest poniedziałkowy poranek!
Przez cztery niewspółpłaszczyznowe punkty A, B, C i D przechodzi przez pojedynczą kulę.
Tak naprawdę mam wielościan, którego rogi są definiowane przez parametryzację, jest wpisany w sferę, której środek chcę zebrać...
1 polubienie
Nie chciałbym opuszczać SW... z równaniem, z którym możesz sobie poradzić!
1 polubienie
Witam
Bierzesz pierwsze 3 punkty: A, B i C → tworzysz płaszczyznę przechodzącą przez 3 punkty i tworzysz okrąg przechodzący przez te 3 punkty, → masz środek, → rysujesz prostopadłą do płaszczyzny przechodzącej przez środek.
Bierzesz D, C i D (a raczej B, jak @Sylk wskazałem), robisz to samo → drugą prostą prostopadłą do drugiej płaszczyzny
Przecięcie 2 linii → środku kuli (jeśli SW pozwala na utworzenie jej za pomocą krzywych...)
Sfera 4 punkty. SLDPRT (138.3 KB)
Uwaga: zadziałało to z przykładem dołączonym w V2020
3 polubienia
Miałeś na myśli B, C i D
1 polubienie
To nie jest złe 
2 polubienia
Trudny początek poniedziałku dla wielu osób
2 polubienia
Więc jestem pod wrażeniem!
2 polubienia
Witam
Inne rozwiązanie...
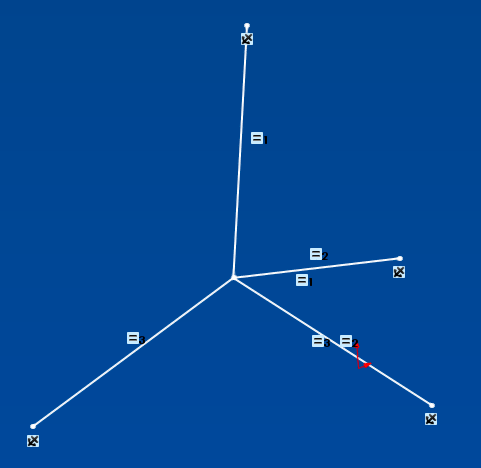
W szkicu trójwymiarowym (3D) narysuj 4 segmenty od dowolnego nieograniczonego punktu P do 4 punktów A, B, C i D. Dodaj relację równości na długościach 4 segmentów i gotowe. P jest środkiem kuli.
3 polubienia
Tak... Spróbuję!
Znacznie łatwiejszy do zbudowania niż to, co proponowałem (ale czuję, że SW dość szybko umieszcza czerwień wszędzie w przypadku modyfikacji).
1 polubienie
Tak, od początku zmienia kolor na czerwony (niemożliwe jest ustawienie równości na 4 segmentach - > na bezpośrednim ograniczeniu)
Działa bardzo dobrze. Musisz tylko umieścić przydatne relacje:
- usunąć wszelkie automatyczne powiązania, które istnieją po utworzeniu segmentów (takie jak zbieżności lub prostopadłości),
- dodać stałą relację do każdego punktu końcowego segmentu (ponieważ współrzędne są znane i stałe),
- Zaznacz wszystkie wiersze w segmentach i dodaj relację równości.
Proszę bardzo.
1 polubienie