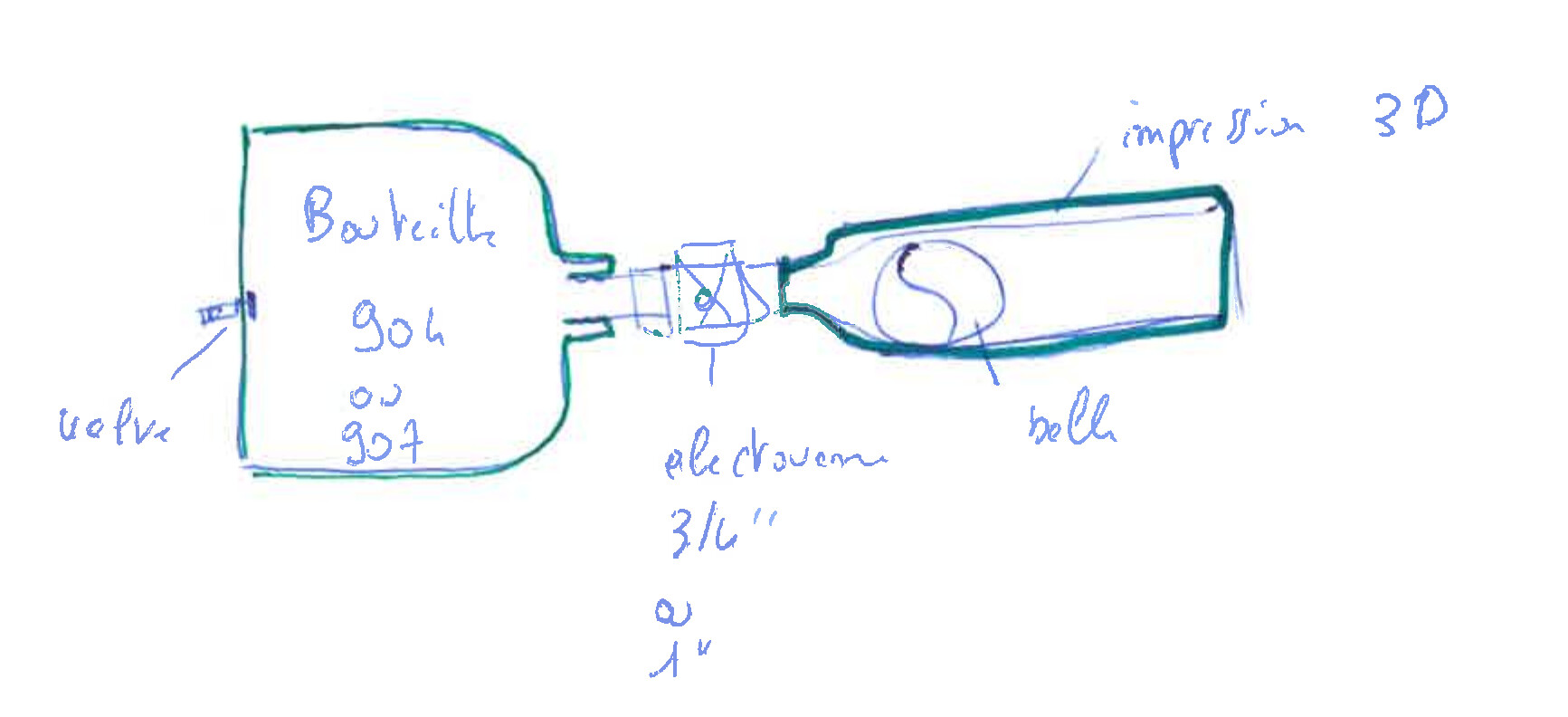
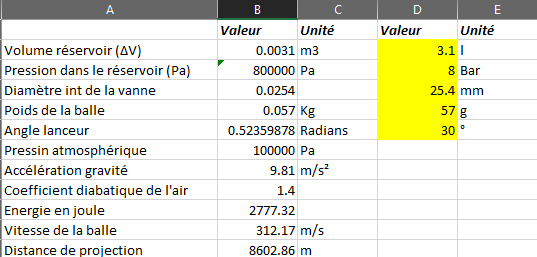
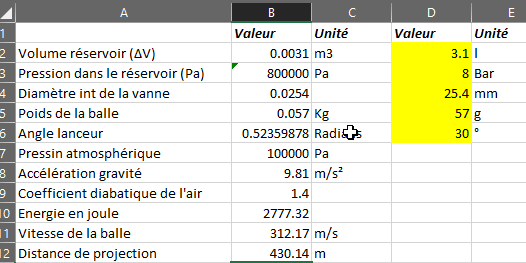
Hello, here is the beginning of the bot's answer, this can help: how much pneumatic power does it take to send a tennis ball 20m?
ChatGPT said:
To send a tennis ball 20 meters with a pneumatic system, several parameters must be taken into account such as the mass of the ball, the pressure, the volume of air, and the friction of the air. Here's a simplified estimate of how much power is needed, looking at the situation from a physical perspective.
1. Estimation of the necessary muzzle velocity
To start, let's calculate the speed a tennis ball needs to reach to travel 20 meters. The basic formula for the distance traveled under a parabolic path is:
d=v2sin(2θ)gd = \frac{v^2 \sin(2\theta)}{g}d=gv2sin(2θ)
Where:
- ddd is the distance traveled (20 m),
- vvv is the initial velocity,
- θ\thetaθ is the launch angle (we will take an optimal angle of 45° to maximize the range),
- GGG is the acceleration due to gravity (about 9.81 m/s²).
At an angle of 45°, sin(2θ)\sin(2\theta)sin(2θ) becomes 1, so the simplified formula for the velocity vvv is:
v=d⋅gv = \sqrt{d \cdot g}v=d⋅g
Let's substitute the values:
v=20⋅9.81≈14 m/sv = \sqrt{20 \cdot 9.81} \approx 14 , \text{m/s}v=20⋅9.81≈14m/s
The ball must be launched with a muzzle velocity of about 14 m/s to travel 20 meters under ideal conditions (without air resistance and without effects other than gravity).
2. Estimating the energy required
The kinetic energy EEE of a tennis ball is given by the formula:
E=12mv2E = \frac{1}{2} m v^2E=21mv2
Where:
- mmm is the mass of the tennis ball (about 57 g or 0.057 kg),
- vvv is the muzzle velocity (14 m/s).
Let's substitute the values:
E=12×0.057×(14)2≈11.1 JE = \frac{1}{2} \times 0.057 \times (14)^2 \approx 11.1 , \text{J}E=21×0.057×(14)2≈11.1J
So the kinetic energy required to throw the ball at this speed is about 11.1 joules.
3. Pneumatic power required
To propel this ball with a pneumatic system, you need to know how much air is needed to provide that energy. Suppose we use a compressed air tank and a mechanism that quickly releases pressure to send the ball.
The power depends on the time it takes to release this energy. If we assume that the energy is released in a fraction of a second (say 0.1 seconds), the power can be calculated by the formula:
P=EtP = \frac{E}{t}P=tE
Let's substitute the values:
P=11.10.1=111 WP = \frac{11.1}{0.1} = 111 , \text{W}P=0.111.1=111W
This means that it would take about 111 watts of power to send the ball 20 yards out in 0.1 seconds.
Conclusion
In summary, to send a tennis ball 20 meters with a pneumatic system, you would need a system that can deliver about 111 watts of power by releasing the energy over a short period of time. Of course, this doesn't take into account losses due to air friction and other factors like the efficiency of the mechanism, but it does give you a general idea of how much power is needed.
)
, that's what I gleaned from the web.
), otherwise I'm very worried about global warming!