Het beste is om er snel een voor jezelf te maken.
En je maakt voor ons een videopresentatie van het resultaat met de hond ![]() natuurlijk
natuurlijk
Er is de wind van de bollen ![]()
Leuke woordspeling, maar sinds wanneer is de Vendée in Bretagne? ![]()
Wees voorzichtig, de Breton is lichtgeraakt, nou hij is Bretoens wat ![]()
Hoi allemaal ![]()
Het antwoord van ChatGPT op @Scofield over de beweging van de kogel na het verlaten van de buis is vaag maar acceptabel: 20 m is inderdaad de orde van grootte van het bereik voor een beginsnelheid van 14 m/s en een vertrekhoek van 45°. Het geëvalueerde pneumatische vermogen is grover en minder interessant...
Wat betreft de Excel-simulatie en een uitwerpsnelheid van 312 m/s, bevinden we ons in het rijk van een vuurwapen.

De grootste moeilijkheid van de ballenwerper is de inschatting van de snelheid die de bal kan bereiken als hij door de buis reist.
De luchtstroom van de tank naar de buis is afhankelijk van de stroomopwaartse druk, maar ook van de vorm en doorsnede van de doorgang door de klep, de lengte van de buis, enz. Er is ook een grote invloed op de openingstijd van de klep, waarbij het doorgangsgedeelte varieert van 0 tot de maximale waarde, met als gevolg een relatief langzame toename van de luchtstroom.
Het andere aspect van het probleem is de toename van de druk in de buis, die zelf afhangt van de beweging van de bal (massa, doorsnede), de speling en de wrijving tussen de bal en de buis. En waarom niet luchtweerstand.
De lengte van de buis zal ook van invloed zijn, in verband met de stroming: het is niet nodig om een lange lengte te plaatsen als de tank de stroming niet aankan.
Ik heb een simulatie geprobeerd met gegevens die mij realistisch lijken, op fysieke basis: luchtstroom door een opening en PFD aangebracht op de bal. Enkele resultaten staan in het bijgevoegde document.
In principe: 17 m/s uitrijsnelheid en 27 m bereik.
Hoeveel vertrouwen kunnen we stellen in een simulatie van dit type? Naar mijn mening geen. ![]()
![]()
Het pb is om te weten of het een goede weerspiegeling is van de werkelijkheid, die pas wordt gevalideerd na het vervaardigen van een prototype en testen.
Hoewel de resultaten niet kunnen worden gegarandeerd, is het mogelijk om de invloed van bepaalde parameters vast te stellen.
In het bijzonder de klep: onder dezelfde simulatieomstandigheden neemt de uitwerpsnelheid toe van 17 naar 22,8 m/s door de openingstijd slechts te verlengen van 0,1 s naar 0,05 s.
Je moet een klep vinden met een opening van het type " pons "...
LanceurBalles.docx (155.4 KB)
Aangezien we de Bretonse vlag overal in Frankrijk zien ![]()
Waar, tot zover voor mij
Wat de baballator betreft, vergeet niet dat een ba-ball geen lood is; Het stuitert terug en behoudt zijn traagheid langer. Een hoge schiethoek zorgt ervoor dat de bal hoger stuitert, maar niet zo ver, een hoek van 45° is optimaal om het bereik met een lagere snelheid te vergroten, maar de bal kan achter het hek terechtkomen, een te lage hoek kan de hond verblinden.
Nee, de " Gwen ha du " is universeel en is over de hele wereld te vinden, lang leve de " Breizh Power "!! ![]()
![]()
![]()
Sommigen zeggen zelfs dat de 1e foto's op de maan in de studio opnieuw zijn gemaakt.

De originele afbeelding toonde ongetwijfeld een Gwen ha du!
" Baballator " neem ik! Niet te veel risico aan deze kant, het doel is om in een hoek van maximaal 30) te schieten, zodat de hond hem vangt bij de 1e of 2e stuiter max, wanneer mijn 4-potige raket passeert.
De " Baballator " moet worden gebruikt om een hindernis in lg te springen.

Als de hond goed kan blazen en correct springen, worden we beloond.
En de snelheid van de Baballator helpt om stroomopwaarts snelheid te geven, omdat de hond snel zal begrijpen dat hij moet duwen om de bal snel te vangen.
Het veld is gras, dus het stuiteren is erg verminderd. En ja, in Bretagne blijft het grasveld groen!
Bedankt @m_blt dit me troost bij de keuze van de tank (belangrijk genoeg) en ook bij de afstanden geschat op de pifometer 20-30-40m max met een druk van 4 tot 10 bar max (waarschijnlijk 4-8 bar max)
Voor het snel openen van de klep aarzelde ik om een goedkope aliexpress-klep te proberen (lucht- of watermagneetventiel van maximaal 10 bar), maar er werd geen openingstijd aangegeven en het is onwaarschijnlijk dat ik zoiets snels als 0,1 s zou hebben!
Een andere oplossing is een handmatig ventiel met een bandencilinder die wordt gevoed door een kraan op de tank en de cilinder wordt geactiveerd door een radiografische afstandsbediening.
En zoals aangegeven, ik hoef alleen nog maar te kopen en te produceren!
De " collega's " van het werk opgelegd door de directie, zijn niet echt collega's geachte heer SAOUT! ![]()
![]()
![]()
Voor sneeuwschoenwandelen zou ik eraan denken als ik op mijn ligstoel met een biertje naar mijn hond kijk springen!
En het doel is dat de launcher verborgen (niet zichtbaar) is, in tegenstelling tot een racket in de hand!
Een gemotoriseerde as en een bewegingsmelder, en 's nachts kun je zelfs indringers afschrikken. Je hoeft alleen maar hoog genoeg te kalibreren om niet tegen de kat of een egel aan te botsen.
Aannamen:
In de loop, adiabatische trekker totdat de loop uit de kogel komt.
We kennen P1, V1 en V2 (V2=V1+Volume van de kanonkamer die is
afhankelijk van de diameter van de kogel en de lengte van de loop)
De trigger is adiabatisch
dus P2=P1(V/V2)^gamma
Dan W=(P2 V2-P1 V1)/(1-gamma)=0,5mV^2
Die geeft bij de uitgang van de loop V van de kogel 220m/s voor een lengte
0.6m kanon
Een andere schatting van de pollepel is Constante druk in het vat = 8b
F=SP=mversnelling
Bij constante acceleratie weten we de duur van de worp:
Kanon = 0.5acct ^ 2
En de uitgangssnelheid =acc*t=240m/s
Daarna wordt de bal alleen nog onderworpen aan zijn gewicht en de
slepen = 0.5rhoSCxV ^ 2 = 0.00113 * V ^ 2
Met een Cd van 0,55 volgens de AI.
Daarna moet je in korte tijd verder gaan
m*acceleration=Drag+Weight en m(V(t+dt)-V(t))=F waarmee je het volgende kunt doen:
bepaal V(t+dt) als een functie van V(t) en F zelf als een functie van
V(t). En als je alle V(t) kent, kun je de coördinaten van de
bal door Positie(t+dt)-Positie(t)=V(t) en je stopt de iteratie
wanneer de hoogte van de positie = 0...
Op deze schaal is het " Breizh Zèle "!
Uitstekend!!!
Hallo
10 dagen later kan het project al door de wind worden weggeblazen...
Om aan de eerste vraag te voldoen, heb ik een Excel-macro geschreven die het fysieke aspect van de ballenwerper simuleert.
Het enige wat u hoeft te doen is de twee bestanden (xlsm en pdf) naar dezelfde map te kopiëren en de Excel-werkmap te openen. Eén klik op de knop met afbeelding en de macro wordt uitgevoerd. In de regel...
Ik heb nog niets gevonden om de hond te simuleren...
LanceurBalles.zip (686.5 KB)
Nee, het is nog steeds relevant, ik wacht tot mijn paar aankopen beginnen met produceren.
En ik zou niet nalaten hier terug te komen en de meest realistische oplossing te kiezen.
Dank u @m_blt voor uw voorstel dat ik nu zal bestuderen.
Bewerken: bovenste macro voor een volledig antwoord, het is een compleet antwoord!
Snelle vraag, waar verwijst het dode volume van de buis naar (een lege kamer waar de lucht zich ophoopt voordat de bal wordt geduwd?)
Moet je er een aantrekken?
Ik stelde me voor om het ventiel aan de uitlaat van de fles te zetten dankzij een adapter M16x1 en G3/4", dan aan de uitlaat van het ventiel direct de loop met 3/4" G en dan conus tot aan de Ø van de kogel en rechte loop.
Ik zie dat dit het bereik veel verandert, afhankelijk van de openingstijd van de klep (+ lange opening betekent niet + lange afstand)
de lengte van de hond (goed om te weten, ik zou ervoor zorgen dat ik hem extensions kan geven voor de test!)
En natuurlijk volgens het dode boek (vandaar de vraag!)
Vanuit het oogpunt van simulatie drukt een van de gedragswetten de relatie tussen druk en volume uit:
p(t) V(t) = p0 V0
waarmee we p(t) = P0 V0 / V(t) kunnen berekenen
Bij de eerste berekeningsstap is het enige bekende volume V(t) V0. Als V0 nul is, wordt er gedeeld door 0 waardoor de berekening crasht. Het zou gemakkelijk zijn geweest om het probleem te omzeilen door een test, met een andere uitdrukking in deze eerste stap: p(t) = p0.
Maar zoals wel vaker het geval is: geen waarborgen...
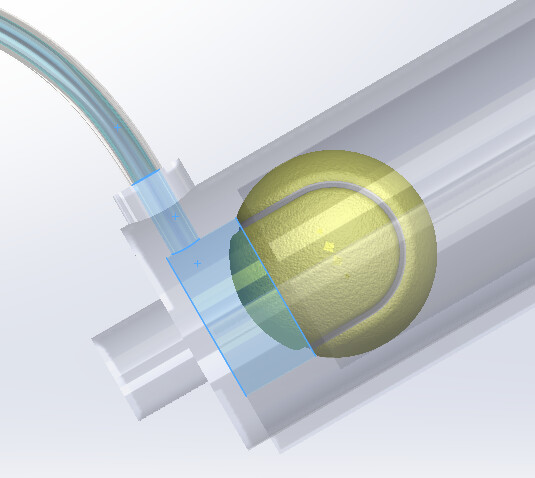
En dan is er in het echte leven noodzakelijkerwijs een dood volume aan de achterkant van de bal, hoe klein het ook is (pijp, kegel beschouwd op de bodem van de buis...). In blauw op de illustratie hieronder.
Ook als het waarschijnlijk in uw belang is om V0 te verlagen voor een snellere drukopbouw.
De twee parameters van openingstijd en slanglengte zijn aan elkaar gekoppeld in de zoektocht naar een optimale uitwerpsnelheid. Een mogelijke benadering is om te simuleren met een lange buis (3000 mm), om te zien dat de snelheid een maximum overschrijdt en vervolgens afneemt.
Het is de positie van de baal bij deze maximale snelheidswaarde die de optimale lengte van de buis bepaalt. Daarna volgt de luchttoevoer naar de tank niet meer...
Resultaat: buis van ongeveer 2000 mm met de overige standaard instellingen!
Hoge snelheid zeker, maar met een drukval in de tank van bijna 1,5 bar. De autonomie van de tank zal twee worpen zijn, een derde zwak, en terug naar de pomp...
Dit alles met de vraag naar de geldigheid van de simulatie en de parameters ervan...