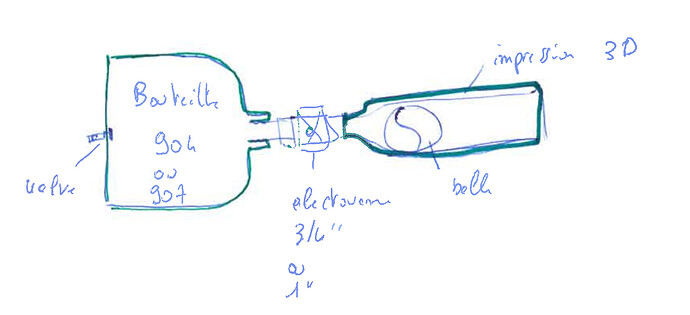
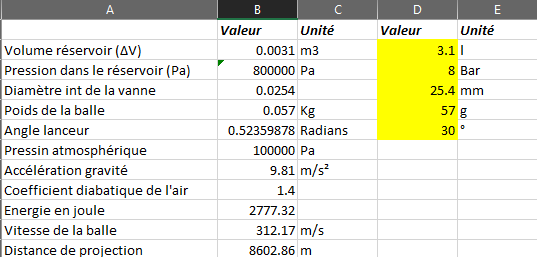
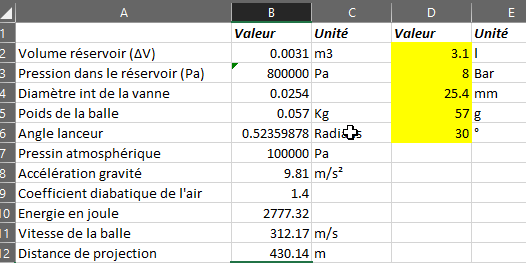
Witam, oto początek odpowiedzi bota, to może pomóc: ile mocy pneumatycznej potrzeba, aby wysłać piłkę tenisową na 20 m?
ChatGPT Powiedziała:
Aby wysłać piłkę tenisową na odległość 20 metrów za pomocą układu pneumatycznego, należy wziąć pod uwagę kilka parametrów, takich jak masa piłki, ciśnienie, objętość powietrza i tarcie powietrza. Oto uproszczone oszacowanie ilości potrzebnej mocy, patrząc na sytuację z perspektywy fizycznej.
1. Oszacowanie niezbędnej prędkości wylotowej
Na początek obliczmy prędkość, jaką musi osiągnąć piłka tenisowa, aby przebyć 20 metrów. Podstawowy wzór na odległość przebytą pod torem parabolicznym to:
d=v2sin(2θ)gd = \frac{v^2 \sin(2\theta)}{g}d=gv2sin(2θ)
Gdzie:
- ddd oznacza przebytą odległość (20 m),
- vvv oznacza prędkość początkową,
- θ\thetaθ to kąt startu (przyjmiemy optymalny kąt 45°, aby zmaksymalizować zasięg),
- GGG to przyspieszenie ziemskie (około 9,81 m/s²).
Pod kątem 45° sin(2θ)\sin(2\theta)sin(2θ) staje się 1, więc uproszczony wzór na prędkość vvv to:
v=d⋅gv = \sqrt{d \cdot g}v=d⋅g
Podmieńmy wartości:
v=20⋅9,81≈14 m/sv = \sqrt{20 \cdot 9,81} \approx 14 , \text{m/s}v=20⋅9,81≈14m/s
Kula musi być wystrzelona z prędkością wylotową około 14 m/s , aby przebyć 20 metrów w idealnych warunkach (bez oporu powietrza i bez oddziaływań innych niż grawitacja).
2. Oszacowanie zapotrzebowania na energię
Energia kinetyczna EEE piłki tenisowej jest określona wzorem:
E=12mv2E = \frac{1}{2} m v^2E=21mv2
Gdzie:
- mmm to masa piłki tenisowej (około 57 g lub 0,057 kg),
- VVV to prędkość wylotowa (14 m/s).
Podmieńmy wartości:
E=12×0.057×(14)2≈11.1 JE = \frac{1}{2} \times 0.057 \times (14)^2 \approx 11.1 , \text{J}E=21×0.057×(14)2≈11.1J
Tak więc energia kinetyczna potrzebna do rzucenia piłki z tą prędkością wynosi około 11,1 dżuli.
3. Wymagana moc pneumatyczna
Aby napędzać tę piłkę za pomocą układu pneumatycznego, musisz wiedzieć, ile powietrza jest potrzebne, aby dostarczyć tę energię. Załóżmy, że używamy zbiornika sprężonego powietrza i mechanizmu, który szybko uwalnia ciśnienie, aby wysłać piłkę.
Moc zależy od czasu potrzebnego do uwolnienia tej energii. Jeśli założymy, że energia jest uwalniana w ułamku sekundy (powiedzmy 0,1 sekundy), moc można obliczyć według wzoru:
P=EtP = \frac{E}{t}P=tE
Podmieńmy wartości:
P=11.10.1=111 WP = \frac{11.1}{0.1} = 111 , \text{W}P=0.111.1=111W
Oznacza to, że potrzeba około 111 watów mocy , aby wysłać piłkę na odległość 20 jardów w 0,1 sekundy.
Konkluzja
Podsumowując, aby wysłać piłkę tenisową na odległość 20 metrów za pomocą układu pneumatycznego, potrzebny byłby system, który może dostarczyć około 111 watów mocy, uwalniając energię w krótkim czasie. Oczywiście nie uwzględnia to strat spowodowanych tarciem powietrza i innymi czynnikami, takimi jak wydajność mechanizmu, ale daje ogólne wyobrażenie o tym, ile mocy jest potrzebne.
)
), w przeciwnym razie bardzo martwię się globalnym ociepleniem!